Square Termini - II
1 , 2 , 3 , 4 , … , 1 5 , 1 6 , 1 7 The first 1 7 positive integers are rearranged into a sequence such that the sum of any two adjacent terms is a perfect square.
What is the sum of the first and last terms of this sequence?
The answer is 33.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
36 solutions
I agree with your answer but not how you got there.
You say: j and z are the first and last number of the rearranged sequence meaning that they have only one term that can be added to them that results in a perfect square.
There is no such guarantee. If it is true (and it happens to be true) then the rest follows, but you need to verify that it's true too.
Log in to reply
16,9,7,2,14,11,5,4,12,13,3,6,10,15,1,8,17 As I can see this question not about numbers, but about logic.
Log in to reply
Hey 16 and 17 can yield perfect sq no. Greater than16 on addition ie 25,36,49 and so on .36 can not be attained since even on adding the two greatest terms in the sequence viz 16 and 17 we get 33 which is still less than 36!!!thus they can yield 25 only and hence only one possible way to get a perfect square from 16 and 17 (under the given set of conditions of the problem) .Thus they should constitute the ends of the chain!!!!
I agree with this; there is no guarantee that the first and last have only one valid neighbor. You can go from the other direction though. That is prove that there exist 2 terms it the sequence that do in fact have only one valid neighbor. Then these two must be the first and last.
Considering that 16 is already a perfect square and there is no zero, its sums must be at least 25. Adding 16+17=33 < 36 means that the largest possible square to form is 25. This means that the sums of 16 and 17 must always be 25, so there is only one possible neighbor for each of them. Therefore, they must be on the ends.
I wrote the numbers 1 to 17, and beside each number, the numbers that could be added to it to form a perfect square. From that list, it was easy to see 16 and 17 were the only two numbers that had exactly one addend and the rest of the sequence was obvious.
Is there a more-general (non-brute force) solution to the "sum of adjacent numbers = perfect square" problem? Do such number sequences have any application?
It seems to me that you have shown that if this can be done then 16 and 17 must be the first and last numbers. But it also seems to me that you have not shown that it can be done. Regards, David
You are amazing
Relevant wiki: Integers - Problem Solving
It's a nice exercise to determine the entire sequence. It can start with 16 or 17 of course, giving 2 solutions that are copies but reversed:
17,8,1,15,10,6,3,13,12,4,5,11,14,2,7,9,16
I had done it that way but accidentally I pressed the button to discuss solutions before putting my answer and it came out that I looked at the solution :(
The most intuitive answer this!
Relevant wiki: Perfect Squares, Cubes, and Powers
This problem can be easily solved in two simple steps.
STEP 1 :
Writing down all the possible perfect squares that can be made and by which numbers.

You can, of course, skip this step if you can remember which perfect squares are associated with each number from 1 to 17.
STEP 2:

Creating a graph.
Connecting the nodes whose sum is a perfect square.
There are two possible paths through the graph but both of them result in the same answer of 16+17 = 33
There is only one path. If you connect 1 and 3, there will be three unconnected nodes 6, 10 and 15. Nice solution.
Log in to reply
They meant backwards and forwards. One and three are associated with each other because they add to make 4, a perfect square, not because they have to go like that for the sequence. There is a redundancy because 1 and 3 are the only ones that, added to another distinct number from one to seventeen, can result in a maximum of three perfect squares (4, 9, 16).
Thank You! Beautiful method beyond brute force--always a welcome solution!
You don't need the graph at all. Once it is found that 16 and 17 have only one possible connection, that's it.
Log in to reply
True if you know there is a solution. Otherwise you have to show that there is a solution.
Log in to reply
There is no requirement for a solution in the question. It is sufficient to show that IF there is a solution THEN the sum must be 33. That is all the question asks, it did not ask for a solution. As it happens there is a solution.
That graph looks exactly like mine. That is how I solved it originally.
Since the highest square number you can make is 25, the numbers 16 and 17 only have one adjacent number, making them automatically at the end. There the answer is 16+17=33
Elegant solution!
Cuts directly to the point. No graphs, no exhaustive list.
-
The least value of perfect square that can be made by two numbers is the least square > 1 (since 1 is the least element, when added to any other element gives > 1 result) which is 4 .
-
The maximum square value that can be made is ≤ ( 1 7 + 1 6 ) which is 2 5 .
So the squares that can be made are 4 , 9 , 1 6 , 2 5
Now we see that the numbers which are between the extreme terms(considering positions) are involved in two pairs which sum to a perfect square.
And the extreme terms are involved in only one pair which sum to a perfect square.
Thus the values that can be extreme terms are greater than or equal to the second highest perfect square term and make the sum of their respective adjascent pairs equal to 2 5 .
So we conclude that 16, and 17 are the only values which are extreme. So the answer is 3 3
16,9,7,2,14,11,5,4,12,13,3,1,8,17,15,10,6 and 16,9,7,2,14,11,5,4,12,13,3,6,10,15,17,8,1 are two more solutions.
Log in to reply
17+15=32 is not a perfect square.
The solution is that 16 and 17 are the only two numbers with only one pair and must be on the ends and sum to 33. No list required. In addition, there is only one list (up to choice of starting end). 1 and 3 have more than two pairs and pair with each other, but pairing 1 to 3 leads to an incomplete list, forcing the 4 - 1 - 8 and 13 - 3 - 6 pairings to be used. The rest are forced by only having two, or at the ends one.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
|
Ingenious!! Overkill, but STILL; very ingenious!!
Is this program very time consuming?
Log in to reply
I wanted a tuple, recursion, yield challenge and this fit the bill. Took about 90 minutes tops to write. Runs in milliseconds
Again with the code that takes more time to write than a simple proof, and is not really a proof until the code itself is proved.
Starting from 16, you can only add up to the perfect square 25 by adding 9 and only 9: So 16 is one of the ends. Starting from 17, you can only add up to the perfect square 25 by adding 8 and only 8: So 17 is the other end of the sequence. Then, 1 7 + 1 6 = 3 3
I have made this comment elsewhere, so I ought to make it here as well. You have shown that if the sequence can be found then 16 and 17 must be the 1st and last numbers of the sequence. But it seems to me that you have not shown that it can be done. Regards, David
Log in to reply
Well, I could write out one such sequence, but the problem asks for the sum of the ends. Therefore the solution should not concern the sequence itself. But, here it is: 16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8, 17 Peace! :)
16 and 17 are the only values that can be combined with only one other number in the given range to make a perfect square. Therefore they must be at the beginning or end of the sequence: 1 6 → 9 → ⋯ → 8 → 1 7 or 1 7 → 8 → ⋯ → 9 → 1 6 Therefore the answer is 1 6 + 1 7 = 3 3 .
Creating the sequence
Because several of the numbers can be combined with two other numbers in the given range, it is easy to generate good parts of the sequence. 1 7 → 8 → 1 → ( 3 or 1 5 ) . 1 6 → 9 → 7 → 2 → 1 4 → 1 1 → 5 → 4 → 1 2 → 1 3 → 3 → ( 1 or 6 ) . ( 1 or 1 3 ) → 3 → 6 → 1 0 → 1 5 → 1 → ( 3 or 8 ) . The only way to patch these together is 1 7 → 8 → 1 → 1 5 → 1 0 → 6 → 3 → 1 3 → 1 2 → 4 → 5 → 1 1 → 1 4 → 2 → 7 → 9 → 1 6 or vice versa.
Largest Squares Impossible wäre 25. 17 ans 16 can Build it Holy wird eine number, so they habe Holy One neighbor.
If we try to put 16 or 17 in the middle with 2 neighbours we have to get 2 perfect squares >16 and >17 because only positive integers are allowed .The only perfect square available is 25, so these numbers can not be in the middle , so they have to be at the end which gives 16+17 = 33.
In this sequence 16 and 17 can only have one pairing, they will be the end pieces.
16 paired with 9 for 25
17 paired with 8 for 25
long way was fun too
Perfect squares can be: 4, 9, 16, 25 Assuming each number can be used only once write this list of all possible pairs that result in perfect cube. It would be clear to see that sequence must either start or end with number 17 (because the only number that can be added to 17 in order to create perfect square is 8).
As soon as you put 17 & 8 in front of the sequence rest of the logic is linear: 17 8 1 15 10 6 3 13 12 4 5 11 14 2 7 9 16
17 can be only adjacent to 8, 8 can be only adjacent to 1, one can be only adjacent 15 etc.
The biggest square that can be made as a result of the sum of two given numbers on the list is 25 since the greater element (17) is 8 units away from the closest square (25) and 19 away from the second closest square and 19 is not an element in the list. So there's only one element to which 17 can be added and form a square therefore 17 is in one of the ends of the list.
The same logic goes with 16 which is 20 units away from the second closest square (without counting itself).
There is no need to determine the entire sequence. The highest square achievable with the numbers is 25. That's because the two largest numbers are 16 and 17, which add to 33, which is below 36, the next square. Now, the perfect square before 25 is 16. Since there's no 0, all this information together means that both 16 and 17 can only be used to add up to 25. Since they can't be in more than one pair, they must be in either the first or last position. Thus, adding them together, the correct answer is 33!
z3 SAT solver can do this for me if I'm lazy:
In [1]: import z3
In [5]: s = z3.Solver()
In [9]: from z3 import *
In [10]: X = [ Int('x%s' % i) for i in range(17) ]
In [11]: X
Out[11]: [x0, x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12, x13, x14, x15, x16]
In [13]: s.check()
Out[13]: sat
In [14]: s.model()
Out[14]:
[x11 = 1,
x0 = 1,
x9 = 1,
x13 = 1,
x16 = 1,
x8 = 1,
x14 = 1,
x2 = 1,
x10 = 1,
x1 = 1,
x6 = 1,
x3 = 1,
x12 = 1,
x15 = 1,
x4 = 1,
x5 = 1,
x7 = 1]
In [17]: for i in range(17):
...: for j in range(i):
...: s.add( X[i] != X[j])
...:
In [18]: s.check()
Out[18]: sat
In [19]: s.model()
Out[19]:
[x11 = 12,
x0 = 1,
x9 = 10,
x13 = 14,
x16 = 17,
x8 = 9,
x14 = 15,
x2 = 3,
x10 = 11,
x1 = 2,
x6 = 6,
x3 = 8,
x12 = 13,
x15 = 16,
x4 = 4,
x5 = 5,
x7 = 7]
In [26]: for i in range(16):
...: s.add(z3.Or ( [ X[i] + X[i+1] == 4, X[i] + X[i+1] == 9, X[i] + X[i+1] == 16, X[i] + X[i+1] == 25 ]))
...:
In [27]: s.check()
Out[27]: sat
In [28]: s.model()
Out[28]:
[x11 = 6,
x0 = 16,
x9 = 13,
x13 = 15,
x16 = 17,
x8 = 12,
x14 = 1,
x2 = 7,
x10 = 3,
x1 = 9,
x6 = 5,
x3 = 2,
x12 = 10,
x15 = 8,
x4 = 14,
x5 = 11,
x7 = 4]
As we can see, x 0 + x 1 6 = 1 6 + 1 7 = 3 3 . There is obviously a symmetric sequence of numbers, and an answer for this would still be 3 3 . I haven't checked for other solutions but the question suggests there is only one correct answer.
Only the numbers 16 and 17 have only 1 way of adding another number below 17 to get a perfect square, because in both cases the perfect square must be 25, and the perfect square 36 is too big (16 + 20 = 36, and 17 + 19 = 36). So these 2 numbers must be the 1st and last numbers of our sequence IF IT IS POSIBLE (WE STILL HAVE NOT SEEN THIS!!). So starting with 17, 17 > (this is the only 'arrow' that I can see on my computer!) > 8 > 1 > either 15 or 3. Then 3 > either 6 or 13. 6 > 10 > 15 which would go to either 10 which is the number that this sequence has immediately come from, or 1 which was the 3rd number of this sequence. So going from 13 as the 5th number of our sequence 13 > 12 > 4 > 5 > 11 > 14 > either 2 or 11. The sequence cannot continue with 11 since this is the 9th number in the overall sequence. Continuing with 2 > 7 > 9 > 16. There should have been more numbers that have not been used yet, and yet we know that 16 can only have 1 number that makes a perfect square below 36. So this cannot be the sequence. So the only other possibility is continuing from 1 with 15. And then 15 > 10 > 6 > 3 > 13 > 12 > 4 > 5 > 11 > 14 > 2 > 7 > 9 > 16. So the complete sequence is 17 > 8 > 1 > 15 > 10 > 6 > 3 > 13 > 12 > 4 > 5 > 11 > 14 > 2 > 7 > 9 > 16. This sequence can be written either way, but in any case the 1st and last numbers add up to 33! Regards, David
Simple,max sum is 33 so 25,16,9,4,1are possible squares ....Now 17 can form a square with only 8 and 16 with 9
P:)
(Finding Sequence bcus Y not?)
Square numbers possible: 1 , 4 , 9 , 16
Since sum of the square numbers possible with adjacent numbers must be a square number,
Possible numbers 1 can add up with: 3 , 8 , 15
Possible numbers 4 can add up with: 5 , 12
Possible numbers 9 can add up with: 7 , 16
Possible number 16 can add up with: 9
So you start from 16... then just fill the rest without repeating numbers
16 , 9 , 7 , 2 , 14 , 11 , 5 , 4 , 12 , 13 , 3 , 6 ,10 , 15 , 1 , 8 , 17
Wwithout found the complete sequence, you can find the extreme in this way, Any number from 1 to 15 have *at least two possibility * to form a square with a number with a number in the sequence 1,2,3 ,...., 17 For example
- 1 + 1 5 = 1 6 , 1 + 3 = 4 and 1 + 8 = 9
- 1 5 + 1 = 1 6 and 1 5 + 1 0 = 2 5
Instead 16 and 17 have only one possibility to form a square with a number in the sequence S = { 1 , 2 , 3 , . . . . , 1 7 }
For example
- 1 7 + 8 = 2 5
- 1 6 + 9 = 2 5
so the sequence has to be start with 17 and finish with 16 (or start with 16 and finish with 17) because if one of these two number are in the between in the sequence cannot continue the sequence
Then the sum of the extreme of the sequence is 1 6 + 1 7 = 3 3
I did know that 17+8 and 16+9 were the only two possible sums including 17 and 16, but I was having trouble creating the full sequence of paired squares, so I finally broke down and used brute force on the TI84 to find my way to an answer. If anyone enjoys playing with programs on the TI-84 , my program is pasted below.
However, as the 17 and 16 have only one pair each, we have our puzzle answer.
If you are getting ready to buy one of the TI-84 graphing calculators, read this article (www.mazes.com/ti-84-ce) to see why recent OS upgrades make the CE a better choice than any other 84. For example, it now has "Cut and Paste" and "Piecewise Functions".
TI-84 program
seq(X=4 or X=9 or X=16 or X=25,X,1,34→L₄
Lbl 0
17→dim(L₂
Fill(0,L₂
17→N
0→D
ClrHome
Lbl 1
D+1→D
If D≤9:Then:Disp N:Else:Output(D-9,9,N:End
If D=17:Pause
{0→L₃
For(A,1,16
If not(L₂(A)) and L₄(A+N:A→L₃(1+dim(L₃
End
If 1=dim(L₃:Goto 0
L₃(randInt(2,dim(L₃→N
1→L₂(N
Goto 1
Comments in approximate order of appearance above:
I use list L₄ to keep track of what the perfect squares are. That list only needs to be created once
Label 0 is the "start all over" or "reset" line number
List L₂ keeps track of what numbers have been used so far. It starts all zeroes.
By logic, I figured out that 17+8 is the only square that includes 17. so I start with N=17 for the first number in the sequence.
The variable D keeps track of how many numbers we have found so far.
Clear the home screen.
Label 1 is the continuation point for each new number to be found
We increment to keep track of how many numbers have been displayed. The most recent value is always in N.
The first nine numbers are displayed with the DISP command. The rest are displayed with OUTPUT.
If D=17, we have found all the numbers, so the program is done. Technically, this line should have been "Then: Pause: Stop: End" but I wanted to save memory, so I break out of the program once it is paused.
List L₃ is used to keep track of all possible numbers that make a square with the current N value. The actual values are stored in positions 2, 3, ... of this list.
The FOR loop tries every possible value (1 to 16)
The IF statement determines if the sum A+N is a perfect square and if the value A has not yet been used. If TRUE, that value is placed into the L₃ list.
After finishing the loop, if L₃ only has one value, the program starts over with line zero
If there are one or more valid values in L₃, one of them at random is moved into the N variable to be displayed next and that value is marked as USED
and the program goes to line 1 to display that value and look for the remaining values
This was a fun little program to write. This is version 2. The first version stored all the numbers in List L1. Eventually, I need to learn how to format ths type of answer. I know how to do it in Quora.
Running through all numbers, (16+1,16+2...), you find that the only way to get a perfect square is 16+9=25=5². Likewise, you find the only solution for 17 is 17+8. Since these two numbers can be added with only one other number to make a perfect square, they cannot be in the middle, and must, therefore, be at the ends. So, the ends are necessarily 16 and 17, so a total of 33.
Note, we have only shown that if there is a solution, it is 33. This does not show there is a solution.
Let's create a graph plotting all 17 points and linking the pairs with sum of 4, 9, 16 & 25.
(This graph is made using
Graph Online
)
So, the answer should be = 16 + 17 = 33
It is not necessary to build the list to answer the question.
Question:
If the numbers 1,2, ...,17 are arranged into a list when each pair of adjacent numbers sum to a perfect square, what is the sum of the first and last numbers on the list?
Answer:
Each number except the first and last must form a perfect square with two other numbers in order to have both a predecessor and successor on the list.
(The question assumes that such a list can be formed in the first place.. This is not required to answer the question hypothetically "if there is a list of consecutive perfect square sums, what numbers must be at the ends?". As it happens, the list does exist.).
Examining the possible pairings, it is discovered that 1 and 3 can be paired three ways (1 with 3,8,and 15, 3 with 1, 6, and 13), and that 16 and 17 can be paired only one way (16 with 9, 17 with 8) while each remaining number can be paired exactly two ways, e.g. 9 can be paired with 16 and 7, 4 can be paired with 5 and 11, etc..
Without forming the list, it is immediately apparent that 16 and 17 must be at the ends of the list and the answer to the question is 3 3
But for completeness here is the graph showing that 16, 17 are unique and that the list is also unique .
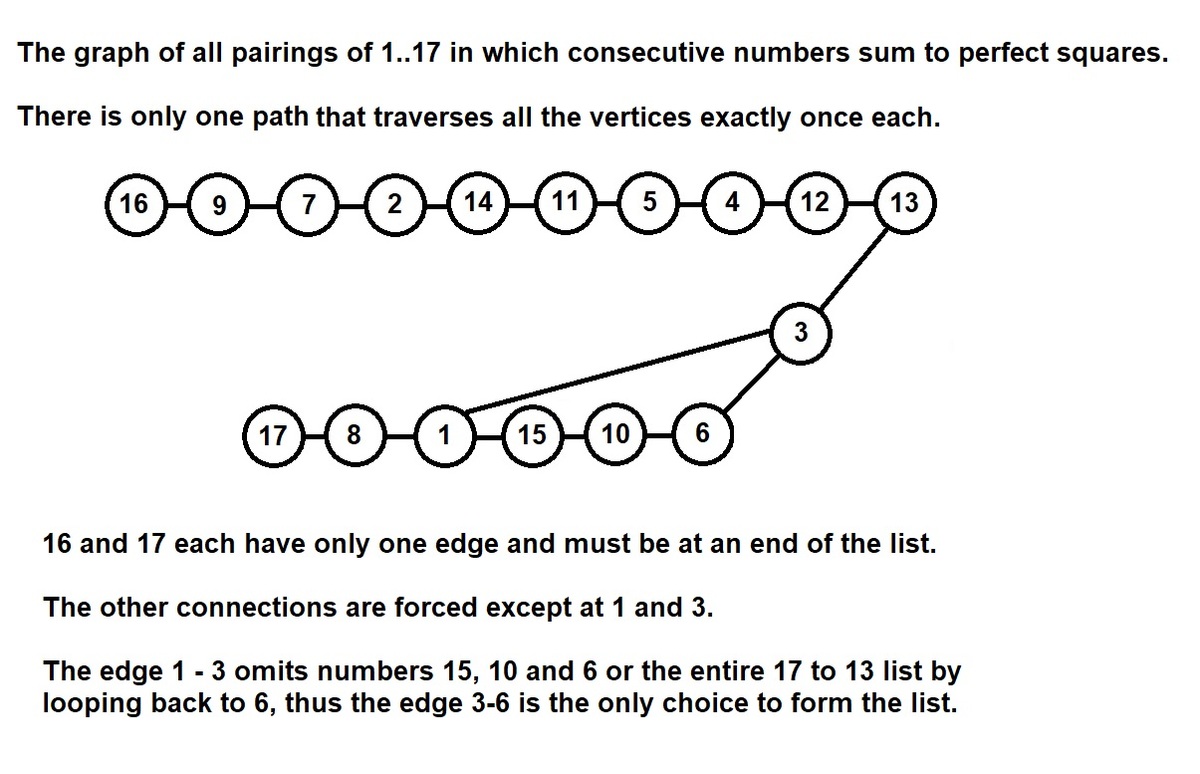
Another post cuts this down to the simple observation that since 25 is the largest perfect square possible, 16 and 17 have only one possible pair, not two or three as in the other cases and are the only possible choices for the ends of the list. That shortens the "examining the possible pairings" above to the bare minimum. (One can't even open the Python editor app quicker than that let alone write any code.)
Here is a video regarding the problem https://m.youtube.com/watch?v=G1m7goLCJDY
Assume that such a sequence is possible. Which you must or the question would not be asked. All numbers within the sequence will have two adjacent numbers. For example 7 will be adjacent to 2, (7 + 2 = 9) and 9, (7 + 9 = 16). The first and last numbers in the sequence will have one adjacent number. The only numbers in the sequence which make a square with only one other are 16, (16 + 9 = 25) and 17, (17 + 8 = 25). So the sum of the first and last terms is 16 + 17 = 33.
I too wrote out all combinations within 1-17 that sum to perfect squares. After doing this I realized you do not need to actually write them all out in a list but simply find which sets contain a nonrepeated number within another set. That is (17,8) is the only set with a 17 and (16,9) is the only set with a 16! So it makes sense 17+16 is the answer as there has to be one beginning and one end. This was a fun problem.
Numberphile has an excellent explonation of the dilution to this problem.
Watch it at https://youtu.be/G1m7goLCJDY
Prime Numbers: 4, 9, 16, 25
1- 3, 8, 15
2- 7, 14
3- 1, 6, 13
4- 5, 12
5- 4, 11
6- 3, 10
7- 2, 9
8- 1, 17
9- 7, 16
10- 6, 15
11- 5, 14
12- 4, 13
13- 3, 12
14- 2, 11
15- 1, 10
16- 9
17- 8
16 and 17 can only add with one other number under 17 to be prime. Therefore, they must be the first and last terms. 16+17=33.
Here's the full string: 17, 8, 1, 15, 10, 6, 3, 13, 12, 4, 5, 11, 14, 2, 7, 9, 16
Primes have nothing to do with it. It is that 16, and 17 have only one pairing inside of 1..17 and can't be in the middle of the list.
Everyone agrees that 33 is the answer. I have not seen an "algorithm" (?) that produces the rearranged sequence immediately. Use the following table to write down the re-arranged series immediately (the values in parentheses pair with the first number to form perfect sums):
1 (8,15)
2 (7,14)
3 (6,13)
4 (5,12)
5 (4,11)
6 (3,10)
7 (2,9)
8 (1,17)
9 (7,16)
10 (6,15)
11 (5,14)
12 (4,13)
13 (3,12)
14 (2,11)
15 (1,10)
16 (-,9)
17 (-,8)
Start with 17 which gives 8 as the next term; go to 8 which gives 1 as the next term (17 is already used); go to 1 which gives 15 as the next term; etc., etc., until the rearranged sequence is written out completely, terminating at 16. Starting with 16 produces the mirror image of the first rearranged sequence.
It isn't even necessary that the list be possible to answer the question. All that is needed16 and 17 are confined to only one possible pair and must be at the ends, while the others have two or more possible pairs, if there is even such a list, as it turns out there is. Who needs an algorithm? (My post includes a graph that covers that in addition to the more essential point.)
The perfect squares possible are 4, 9, 16, and 25. Since 16+17=33 is the biggest possible sum in the series, 36 is not possible.
The sequence must start or end with 17, since it's bigger than 16 and therefore only appears on one sum equalling 25 (17+8).
It must also begin or end with 16, since 9, 16 is the only pair where 16 appears. (16+n>16 for the set of natural numbers.)
Now we know the answer is 33, but I decided to find the full sequence.
I quickly jotted down all possible sums for each square:
4: (1, 3)
9: (1, 8) (2, 7) (3, 6) (4,5)
16: (1, 15) (2, 14) Etc.
25: (8, 17) (9, 16) (10, 15) Etc.
If you start the sequence with
17, 8...
you can quickly refer to the list and see that 1 must be the next number because 1, 8 is the only other pair involving 8 besides 8, 17.
So:
17, 8, 1...
The next number can be either 3 or 15. Using 3 fails:
17, 8, 1, 3, 6, 10, 15... Nowhere to go after that.
Again, just referencing possible pairs from my list, I try again with these first 4 in the sequence:
17, 8, 1, 3, 13, 12, 4, 5, 11, 14, 2, 7, 9, 16 terminates before all 17 digits are used.
Trying with the other first-four-digits possibility goes like this:
17, 8, 1, 15, 10, 6, 3, 13, 12, 4, 5, 11, 14, 2, 7, 9, 16.
All 17 digits present and accounted for here.
First and last in the sequence have a sum of 33.
Too long. Once one finds that 16 and 17 are the only two that have only one pairing, and must be at the ends, you are done.
starting with 17 -- 17 8 1 15 10 6 3 13 12 4 5 11 14 2 7 9 16 alternatively we may also start with 16
This does not establish that 33 is the ONLY possible answer.
Log in to reply
I just determined the entire sequence and concluded that 33 is the answer.And there is no other way you could do it. However after your comment I thought a bit more over this and realized that all the numbers from 1 to 15 may be added within the set to give either 4,9,16 or 25 as sum but 16 and 17 can only give 25 as a sum. Which means they cannot be in the middle of the series. Well that leaves 33 as the ONLY possible answer.
The two numbers that are at the start and end of the sequence will only need to be able to generate one perfect square each, since they are only going to be added with one other number (the second number and the second to last number). While this is a fine condition for any of the numbers, it is necessary for two of them, 16 and 17, for the following reason:
Any perfect square that you reach via adding to either of 16 or 17 will be higher than the original number (since 0 is not in our sequence). The first perfect square that is above 16 and 17 is 25 : 5 2 , followed by 36 : 6 2 and then a bunch more.
Except 36 is 19 away from 17, and 19 is not in our sequence. And 36 is 20 away from 16, and 20 isn't in our sequence either. So 36 cannot be reached by adding anything in our list to 16 or 17.
So the only number that can be put on the side of 16 is the one that will reach 25 when added to 16. Namely, 9.
And the only number that can be put on the side of 17 is also the one that will reach 25 when added to 17. Namely, 8.
And those are the only numbers that can be placed on either side of 16 and 17 because any other numbers will result in a sum above 16, that is not 25, and is below 36. So they will not be perfect squares.
So if there is more than one number on either side of 16 or 17, then one of those sums will not be a perfect square. So there can only be one number on either side of each of 16 and 17. And the only positions that only have one other number added to it are the first and last positions.
So 16 and 17 must occupy the first and last positions.
Solution: 1 6 + 1 7 = 3 3
The final sequence is: 1 6 , 9 , 7 , 2 , 1 4 , 1 1 , 5 , 4 , 1 2 , 1 3 , 3 , 6 , 1 0 , 1 5 , 1 , 8 , 1 7 (it's not that hard to work it out, and quite fun actually)
The numbers at the start and finish of the sequence must be 16 and 17.
This is because, the closest possible perfect squares to be made with these 2 numbers are 25 and 36.
Hense, 1 7 + 8 = 2 5 and 1 7 + 1 9 = 3 6 . But, as we can see, the term 1 9 is not on the list, and since are no other bigger numbers than 19 on the list, the only perfect square that you could make with 17 is 25. Since there is only one possible solution, 17 must be on one of the ends of the list, as no other in the list is being added to 17 makes a perfect square.
This is the same for the number 16.
1 6 + 9 = 2 5 and 1 6 + 2 0 = 3 6 . The term 2 0 is not on the list though, and since are no other bigger numbers than 20 on the list, 16 has only one solution, being added to a number to make a perfect square.
Other numbers will have solutions though, such as 10 and 1 for 15. 1 5 + 1 = 1 6 and 1 5 + 1 0 = 2 5 .
Therefore, 1 6 + 1 7 = 3 3
At first, I thought there was no such list as this one, but even if there wasn't a list like this one, 16 and 17 would have been the first and last numbers.
It is not necessary to build the sequence, only to find that 16 and 17 have only one pairing, and are the only numbers with only one pairing, and therefore must be at the ends. Since they are the only two there are not multiple solutions.
Firstly, notice that any sum can't be more than 1 6 + 1 7 = 3 3 since 1 6 and 1 7 are greatest numbers we can add. Therefore, we can't use perfect squares greater than 5 2 = 2 5 because next perfect square is 6 2 = 3 6 , which is more than we can get.
Secondly, consider that 1 7 and 1 6 can only be a part of 2 5 since previous perfect square is 4 2 = 1 6 , and the fewest number we must add is 1 . Consequently, we can only add 8 to 1 7 and 9 to 1 6 to get 2 5 in both cases.
But as 1 7 and 1 6 can have an only adjacent number, they must be on the sequence edges. So these are the first and the last number, and their sum is 1 6 + 1 7 = 3 3
This can have a graph theory solution, which is illustrated well in this video
Relevant wiki: Integers - Problem Solving
The amount of perfect squares that can be constructed using 2 different terms from 1 to 17 are 4 (4,9,16,25).
j and z are the first and last number of the rearranged sequence meaning that they have only one term that can be added to them that results in a perfect square. The first 15 positive integers have more than 2 or more terms that can be result in a perfect square, an example of that is 1 5 + 1 0 = 2 5 and 1 5 + 1 = 1 6 or 3 + 1 3 = 1 6 and 3 + 6 = 9 . Using this information we can determine that 16 and 17 only have one term than be added with them that result in a perfect square. 1 6 + 9 = 2 5 and 1 7 + 8 = 2 5 . This leads to that if 16 and 17 are the first and last term of the rearranged sequence their sum is 1 6 + 1 7 = 3 3 .