Square with 2 on a Side

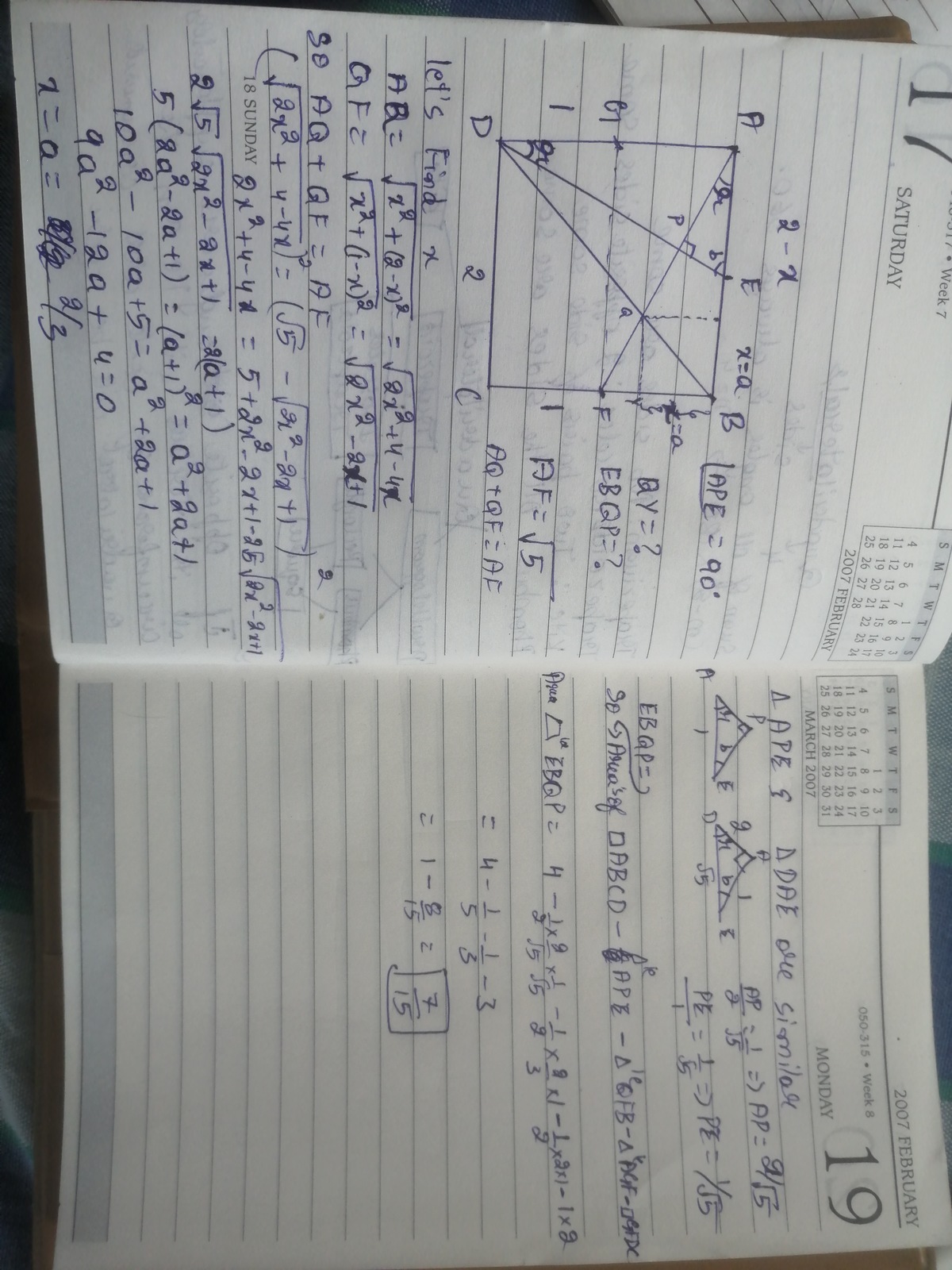
Let Vertex B be at coordinate (0,0), the equations for $\overline{AF}, \overline{ED}$ and $\overline{DB}$ are $\\y=-2x+2, y=\frac{1}{2}x+1$ and $y=x$ respectively $\\$ From here, the coordinates of P and Q are located at the intersections.

P such that $\frac{1}{2}x+1=-2x+2 \rightarrow x=\frac{2}{5}$ and substituting back in gives $y=\frac{6}{5}$ , and

Q such that $x=-2x+2 \rightarrow x=\frac{2}{3}$ and substituting back gives $y=\frac{2}{3}\\$

The Area $EBQP = ABF - AEP - BFQ = \frac{1}{2}(1)(2) - \frac{1}{2}(1)(\frac{2}{5}) - \frac{1}{2}(1)(\frac{2}{3}) = 1-\frac{1}{5}-\frac{1}{3} = \boxed{\frac{7}{15}}$

7/15

This can't be just level 2 geometry problem!