Squared Away!

The distance from the line $x+y-12=0$ to the origin is $\frac{12}{\sqrt{2}}>8$ , exceeding the radius of the circle $x^2+y^2=64$ , so that they fail to intersect. The answer is $\boxed{99}$

We have $x^2 + y^2 = x^2 + (12-x)^2 = 2x^2 - 24x + 144 = 2(x - 6)^2 + 72 = 64,$ which implies $(x-6)^2 < 0$ ; this equation has no real solutions.

The solutions are actually $x,\ y = 6\pm 2i$ , and $xy = (6+2i)(6-2i) = 6^2 - (2i)^2 = 36+ 4 = 40.$ However, these solutions are not real numbers as was required.

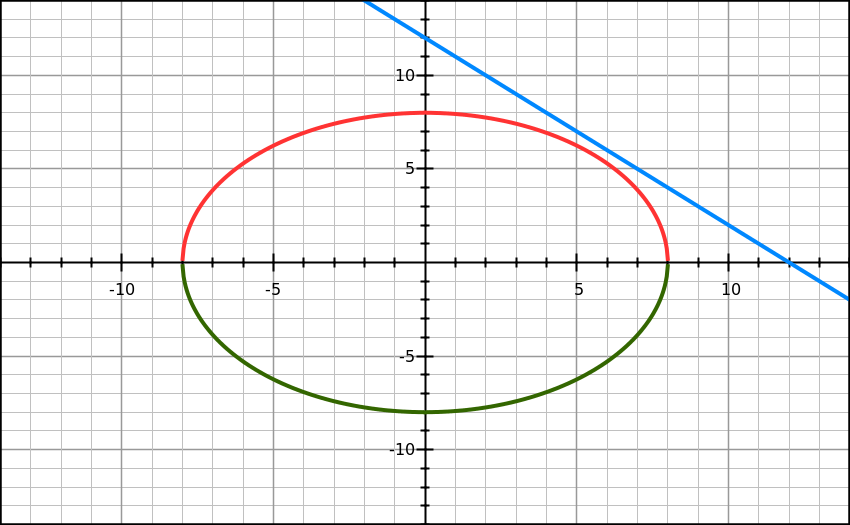Clearly the line $x+y-12=0$ and the circle $x^2+y^2-64=0$ do not have any ordered $(x,y)$ in common. Hence , no solutions. $\textbf{OR}$ Put $y=12-x$ in the second equation. $\implies x^2+(12-x)^2=64$ $\implies x^2-12x +40=0$ whose discriminant $=144-160=-16<0$ hence no real $(x,y)$ exist. $\textbf{OR}$ $xy=\dfrac{(x+y)^2-(x^2+y^2)}{2}=\dfrac{144-64}{2}=40$ But we know:- $(x-y)^2\geq0 \implies xy\leq \dfrac{(x+y)^2}{4}=36$ which rules out our case of getting $xy=40$ . $\therefore$ answer is $\boxed{99}$ .

This got me! Eventually I came up with the answer of 99.

If we "squared away". we will get that $xy = \frac{1}{2}(12^2-64) = 40$ . Using Vieta's Formula, we will get that X and Y must satisfy the equation $a^2-12a+40 = 0$ , or simply $(a-6)^2+4 = 0$ , which is not possible in set of real number.

$x+y = 12\implies y=12-x$

Substitute this into the second equation, and we get:

$x^2 + (12 - x)^2 = 64$

$2x^2 - 24x + 84 = 0$

$x^2 - 12x + 42 = 0$

Solving for $x$ :

$x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

$= \dfrac{12 \pm \sqrt{(-12)^2 - 4(1)(40)}}{2(1)}$

$= \dfrac{12 \pm \sqrt{-16}}{2}$

From here, we can see that the two solutions will be complex. Since $x$ and $y$ are not real numbers, there is no need to continue calculating anymore, as the answer is $\boxed{99}$

Alternatively, you can use the discriminant for quadratic equations $b^2 - 4ac$ to determine that there are no real roots that satisfies the system above.