Squared number!

Define an integer $n = \overline{\cdots ab}.$ That is, $n$ is an integer whose last two digits are $a$ and $b.$ Now consider this integer mod 100 (this is a way of looking at just the last two digits of the number):

$n \equiv 10a+b \pmod{100}$

Square it:

$\begin{aligned} n^2 &\equiv (10a+b)^2 \pmod{100} \\ n^2 &\equiv 100a^2+20ab+b^2 \pmod{100} \\ n^2 &\equiv 20ab+b^2 \pmod{100} \\ \end{aligned}$

Suppose that this number has all odd digits. The tens digit of $20ab$ is always even, and so the tens digit of $n^2$ can only be odd if the the tens digit of $b^2$ is odd. Also note that if $b^2$ is odd, then $b$ must be odd. So the possibilities for $b^2$ are $\{1,9,25,49,81\}.$ If $b$ is odd, then the tens digit of $b^2$ is always even! This is a contradiction! Thus, $n^2$ can only have all odd digits if it is less than 10.

Let's put the squared number to (10a + b)(10a + b). We don't care how big the number a is going to be. However, the number b is going to be only one digit. So, we take this simplified (10a + b)(10a + b) and make it into some long piece which is 100a a + 20ab + b b. Well b needs to be an odd number, because b * b has to be an odd number. (Even number times even number equals even number, odd number times odd number equals odd number.) In this case, b is one digit and an odd number, so it only gets to be 1 or 3 or 5 or 7 or 9. So, we all want to make these (1, 3, 5, 7, 9) into a squared number. 1 * 1 = 1, 3 * 3 = 9, 5 * 5 = 25, 7 * 7 = 49, 9 * 9 = 81 But 25 contains an even number(2), 49 has 4, and 81 has 8. So, that leaves me with only 1, 9.

An odd number is always of the form (2m+1), where m=1,2,3,...... Now the square of this form can be written as (8k+1) where k=1,2,3..... This implies that the last digit has to odd. We can express k=a+(10 b)+(100 c)+.....as 'k' is any positive integer. But 'k' is multiplied by 8. This makes the other digits even, as the sum of even numbers is even. Hence no squared number except 1 and 9 (single digit number) has its all digit odd.

Write $N = 10a + 5b + c$ with $b = 0,1$ and $-2 \leq c \leq 2$ . Then $N^2 = 100a(a+b) + 20(ac+b^2) + 10bc + (5b^2 + c^2).$ The last digit is odd iff $5b^2 + c^2$ is odd, i.e. either $b$ is odd or $c$ is odd (but not both).

The second-last digit is odd iff $bc$ is odd, i.e. both $b$ and $c$ is odd.

Clearly, these conditions cannot both be true.

Let's try recursion!

Clearly, there are no numbers below 10 that works. Now, let's look at 10-19. a number n between 10 - 19 can be written as (10 + x), thus n^2 = [100 + 20x] + x^2

No matter what, the sum of the digits in the bracket will always have an even middle number (100, 120, 140, ..., 280) All of them end in 0, so they must also have an even final number.

Now, here's the fun part! In order for n^2 to have all odds digits, the final 2 digits of x^2 must be odd (and from 0 to 9, this means all digits must be odd), in order to make the total sum have an odd middle and final number (note that the final digit of the sum in bracket being 0 is important!). However, since n is between 10 and 19, x must be between 0 and 9! We know that this is impossible! (Really, 1^2 and 3^2 are 01 and 09) Thus, it is impossible for n from 0 to 19! (Note that we've proven something stronger -- we've proven that it's impossible for n from 0 to 19 to end with 2 odd digits )

Let's keep going, n from 20 to 29? n = (10 + x) for some x from 0 to 19; n^2 = 100 + 20x + x^2, and x^2 must have an odd final and middle digit for the sum to be so too.

But, we've proven that that's impossible as well!

This can be continued indefinitely, and thus, by recursion, this is true for all positive integers. Then, since -x^2 = x^2, it is also true for all integers.

An odd number is a number by the form 2n+1, where n is 1,2,3,4. The power of an even number is an even number. The power of an odd number is odd. The power of an odd number is (N x N-1) + N An odd number multiplied by an even number is always an even number, with the first digit even and the last even, plus the odd number equals an odd number with the first digit even and the last one odd. Hope you've understand, I don't know what did I've just type there :)

Let n be a perfect square If n is even then at least its last digit is even If n is odd then sqrt(n) is odd then sqrt(n)=2k+1 therefore n=(2k+1)^2=4k^2+4k+1 But n-1 is a multiple of 4 so its two last digit are both even so n has last digit odd (because +1) and before-last digit is even because adding one to the last digit won't make it exceed 9 (it can only be 0 2 4 8) so not all digits of n are odd, n has at least one even digit Note: n has at least two digits (we ommitted the case of 1 and 9)

Let $p$ be the number whose square is composed of all odd digits. We can write $p^2$ in the following way:

$p^2 = 10^na_np + 10^{n-1}a_{n-1}p + ... + 10^2a_2p + 10a_1p + a_0p$

Where $n \in \textbf{N}, n > 0$ and $a_n$ is given by a map of the set {0,1,2,3,4,5,6,7,8,9}.

We can factor out $p$ from the following expression, as well as write an expansion equal to $p$ .

$p^2 = p(10^na_n + 10^{n-1}a_{n-1} + ... + 10^2a_2 + 10a_1 + a_0)$

$p =10^na_n + 10^{n-1}a_{n-1} + ... + 10^2a_2 + 10a_1 + a_0$

If we can prove for all $n \in \textbf{N}$ , where $n > 0$ , that the expansion of $p$ has at least one even digit, then such a $p$ does not exist. We will try to prove the contrapositive.

Assume such a $p$ exists, then there does not exist an $n \in \textbf{N}$ where $n > 0$ s.t.

$10^na_n + 10^{n-1}a_{n-1} + ... + 10^2a_2 + 10a_1 + a_0$

does not have an odd digit.

It is clear to see $10^n$ will always have an odd digit as it's leading digit. It is also clear that any linear combination of $10^n$ terms multiplied by an odd number will also be odd.

If a linear combination of $10^n$ is multiplied by an even number, the resulting number will have all even digits, and will therefore be even. We now have the equation...

$p^2 = p \times ($ even number $)$

which will always yield an even number for $p^2$ , therefore such a $p$ does not exist.

Here's how I solved the problem graphically:

1. Graph the function $f(x)=x^2$ :

2. Make a table that give $f(x)=x^2$ for every positive integer $x$ :

Now look through the table. Notice how even if $x$ has all odd numbers, $f(x)$ does not. Continue looking through the table until you hit 100:

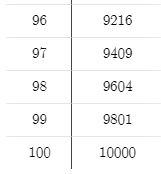
Since no positive integers between 1 and 100 has a value $f(x)=x^2$ that is all odd digits (other than 1 and 9), then there cannot be such a number for any other positive integer beyond 100.