Squares
You have a grid containing the numbers 1 - 100 as shown below, all in order, except that 13 is switched with 40, (in red).
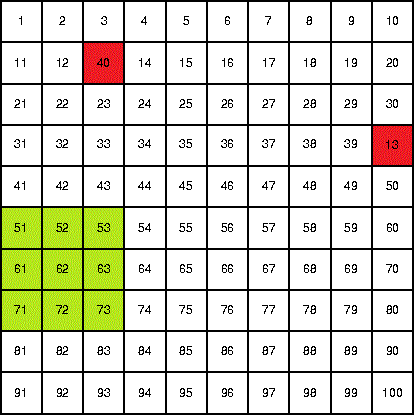
Now for the question...
How many ways can you pick two different groups of 9 numbers (like the one in green above) such that the sum of the 9 numbers inside is the same for both of them?
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are 6 4 possible 3 x 3 grids, and from left to right on the top, their sums are 1 0 8 , 1 1 7 , 1 2 6 , ....
Similarly, each row of 8 such 3 x 3 grids is an arithmetic progression that increases by 9 each time... The 4 0 has had 2 7 subtracted, so any 3 x 3 grid three to the left of any 3 x 3 grid containing the 1 3 will suffice. There are 3 such grids.
By the same argument, for any 3 x 3 grid containing the 4 0 , a corresponding 3 x 3 grid can be found 3 to the right of it. And there are 6 such grids.
Finally we have the box containing 13 in the lower right matching the box containing 40 in the top middle.
So in total we have 6 + 3 + 1 = 1 0 ways.