Squares!

Probability Level 2

How many squares are in the diagram above?

The answer is 56.

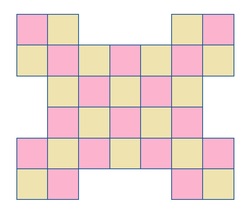
8 solutions

Kenny Lau
Jul 16, 2014

Number of squares with side length 1 = 7x6-2-2-3-3 = 32
Number of squares with side length 2 = 4+3x4 = 16
Number of squares with side length 3 = 2x3 = 6
Number of squares with side length 4 = 2
Total = 32+16+6+2 = 56

I think you have not consider all square

naveen kumar - 6 years, 5 months ago

Can you explain with more details?

Krishibid Hossain - 6 years, 11 months ago

I already explained it in the comment section.

Jobayer Mahmud - 6 years, 11 months ago

please can u explain in detail

Manasa Nagesh - 6 years, 11 months ago

I already explained it in the comment section.

Jobayer Mahmud - 6 years, 11 months ago

i dnt agree with yr answer
what i think correct answer is 59 squres

there are 39 square in the bigger square + there are 20 squares at the corner so total no of squares are 59

Aman Amritesh - 6 years, 11 months ago

I already explained it in the comment section.

Jobayer Mahmud - 6 years, 11 months ago

try to find the square from 1x1 -> maximum size (4x4) we can divide this into 5 fragments, 4 corners (each 2x2) and the center (4x5) 1x1: it's the total area = 4x2x2 + 4x5 - 4 = 32; 2x2: 4 corner + square in the center = 4x3 = 16; 3x3: only in the center = 3x3 = 6; 4x4: only 2 squares; Therefore we have 56 squares

Nguyen Thien Vy - 6 years, 11 months ago

is there any generalized formula to find number of squares in a rectangular grid?

Raj Inamdar - 6 years, 11 months ago

I don't know if there's a written formula for this or not but I use this for myself. For each big grid (5 * 4 grid and the 2 * 2 grid) u can consider n * m grid. Number of squares with side length x is (n-x+1)*(m-x+1). This means the number of squares in the 5 * 4 grid= 5 * 4+4 * 3+3 * 2+2 * 1+1 * 0= 40 Number of squares in 2 * 2 grid= 2 * 2+1 * 1+0 * 0=5 repeated in 4 grids then u have 20 so the sum is 60 but u counted 1 * 1 grid twice in 4 places so it's 60-4=56

Mohamed Wafik - 5 years, 8 months ago

It took the center 5*4 rectangle as square and got 57.

Chitranshu Vashishth - 6 years, 11 months ago

always remember... rectangle is not a square... square always has 4 equal sized sides...

Tahir Wahab - 6 years, 11 months ago

57 IS CORRECT ANSWER

Nitin Nayak - 6 years, 11 months ago

nope, if you did include the whole box in the middle, that's where you committed the mistake. The whole box is 4x5 grid, which makes it a rectangle not a square, i think that was the twist in this question.

Adrian Hansen - 6 years, 11 months ago

all no of squares =57

Hamsa Kallambalam - 6 years, 10 months ago

number of squares with side length 4= 4 ,,,pls recheck,,!!

Sunil Kumar - 6 years, 11 months ago

Number of 4x4 squares = 2

Jobayer Mahmud - 6 years, 11 months ago

sorry itsk

Sunil Kumar - 6 years, 11 months ago

Harish Sasikumar
Oct 8, 2015

Total squares = number of squares in the central figure + 4*Number of squares in a corner figure - number of squares in common = (4x5 + 3x4 + 2x3 + 1x2) + 4(2x2+1x1 ) - 4

Luke Nelson
Jul 17, 2014

Okay, so first off we can easily simply count from top to bottom the squares with side length one. You should get 32. Then the squares with side length 2 need to be counted. The 4 corners, plus the 3 rows of 4 length 2 squares need to be counted from the rectangle in the center (4+3*4). Then the 2 rows of 3 length 3 squares are counted in the middle (3*2). Lastly the two 4 length squares in the middle must be counted (2). Giving us: (32+4+(3*4)+(3*2)+2)=56

Erich Krupp
Oct 8, 2015

32 squares (1/1).............. 16 squares (2/2)............. 6 squares (3/3)........... 2 squares (4/4)...............= 56................square overlaps

Aya Alaa
Sep 25, 2014

squares which have area =1 =>5×4+3×4=32

squares which have area =4=>4+4×3=16

squares which have area=9=>2×3=6

squares which have area=16=>2

the sum =32+16+6+2=56

Jobayer Mahmud
Jul 18, 2014

Please don't be confused about square. It is defined as having all sides equal, and its interior angles all right angles (90°). From this it follows that the opposite sides are also parallel.

As 4 sides of a square must be equal, therefore 1x2, 1x3, 1x4, 1x5, 2x1, 2x3, 2x4, 2x5, 3x1, 3x2, 3x4, 3x5, 4x1, 4x2, 4x3, 4x5 are rectangles but not squares.

Only 1x1, 2x2, 3x3, 4x4 are squares.

Here, Number of 1x1 squares = 32

Number of 2x2 squares = 16

Number of 3x3 squares = 6

Number of 4x4 squares = 2

So total number of squares = 32+16+6+2 = 56

Rishabh Gupta
Jul 17, 2014

i counted all, they were 56

how u count it.... can u explain

Libra Khan - 6 years, 11 months ago

oh yeah! it's easy. first count all small squares, then all which can be formed using 4 small squares, then all which can be formed using 9 small squares, then 2 more big squares which can be formed using 16 small squares. :D

Rishabh Gupta - 6 years, 11 months ago

I already explained it in the comment section.

Jobayer Mahmud - 6 years, 11 months ago

Aseem Sinha
Jul 16, 2014

How to look for squares with side length = 1 ?

You do it by shifting in one particular direction and simultaneously counting the number of squares.

Similarly for square with side length = 2, 3, 4, 5, first move in a particular direction ( say left to right) and when you have reached the point from where you can't further, move one step upwards and then to the left. Continue this process with all the squares with different side length till the point when it is not possible to move any further. In other words, you have counted all the squares.

Aseem Sinha - 6 years, 11 months ago

An easy way to count the squares with side length $1$ is to compute the area of the rectangle with the gaps filled in: $6 \times 7 = 42$ . Then count the missing squares, which are $2 \times 2 + 2 \times 3 = 10$ , and subtract them from the area, giving $32$ squares.

Zarak K - 6 years, 11 months ago

Squares!

The answer is 56.

8 solutions

0 pending reports