SQUARES
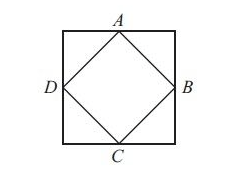 Points ABCD are midpoints of the sides of the larger square. If the larger square has area 60, what's the small square's area?
Points ABCD are midpoints of the sides of the larger square. If the larger square has area 60, what's the small square's area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
We can split the square into 8 triangles by adding one line that runs down horizontally down the center of the big square and one line that runs down vertically down the big square also. Thus, we will find that the the big square has 8 triangles while the small square has 4 triangles. Since all the triangles are similar, this proves that the smaller square is half that of the big square
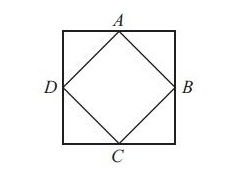
By drawing AC and BD, it becomes clear the figure is built from eight triangles; they must be congruent, because they share angles and sides. The inner square is built of four of these and must have half the surface of the outer.
The side’s ratio is (√2/2). So by similarity the area ratio is (√2/2)2 = ½. So the area of the smaller square is 30.
The side of bigger square is root 60. So diagonal of smaller square is root 60. so area is 60/2 = 30
Consider the large square's side=2a. The area of large square=(2a)^2=60. Join BD. We know that the length of the diagonal of the small square=a side of the large square. The area of a square using diagonal length is 1/2d^2. =1/2×(2a)^2 =1/2×60 =30
I solved it applying the Pythagoras theorem to one of the triangles formed at the angles of the outer square : calling a the side of the outer triangle and b the side of the inner, we have b = a 2 + a 2
That's right, since the sides are in the ratio 2 : 1 , the area is in the ratio 2 : 1 .
Square interior angle for all sides=90° Given=60° Remaining=90°-60°=30°
i know that the outer square is half of inner square so....