Squares all around
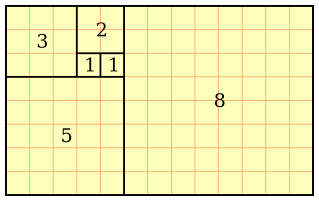
 In the above rectangle, all the smaller shapes are squares. If the two green squares in the center each have a side length of 1, what is the area of the rectangle?
In the above rectangle, all the smaller shapes are squares. If the two green squares in the center each have a side length of 1, what is the area of the rectangle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Nice Gif!!!!
oh what a answer
nice solution!
Fibonacci squares comes to mind.
Denoting the length of green squares as F 1 , F 2 , the brown square: F 3 , blue square: F 4 , purple square: F 5 , red square: F 6 . So the answer is simply ( F 6 + F 5 ) × ( F 5 + F 4 ) = F 7 × F 6 = 1 3 × 8 = 1 0 4 .
The generalization is: for a total of n squares used in the Fibonacci squares, the area is F n + 1 F n (thus proving the identity k = 1 ∑ n F k 2 = F n + 1 F n geometrically).
Great solution
Use Fibonacci Sequence
0, 1, 1, 2, 3, 5, 8
Nice observation :)
The first number of the Fibonacci sequence is 1, not 0 though :-)
We want to find the area of the entire rectangle.
Side of Red Square X (Side of Red Square + Side of Purple Square)
We know that the green squares are each 1 and that the orange square must have a side length of 2.
Then, the Blue must have Green + Orange, or 3.
Purple is 2Green + Blue = 5
Red is Orange + Green + Purple = 8
So going back to our first equation,
WE replace into this Side of Red Square X (Side of Red Square + Side of Purple Square)
To get: 8 X (8+5) = 8 X 13 = 104
Good approach. Keep it up!
Really good explanation. Hats Off!
This is a piece of ice cream. Just draw a diagram and label the sides correctly. Drawing the correct diagram is half of the solution.
Fibonacci explained :). Answer is 104
Green 1, orange2, blue3, purple5, red8 so 8*13=104
Why not prove it with a gif?
Let A be the total area.