Squares and Circles!
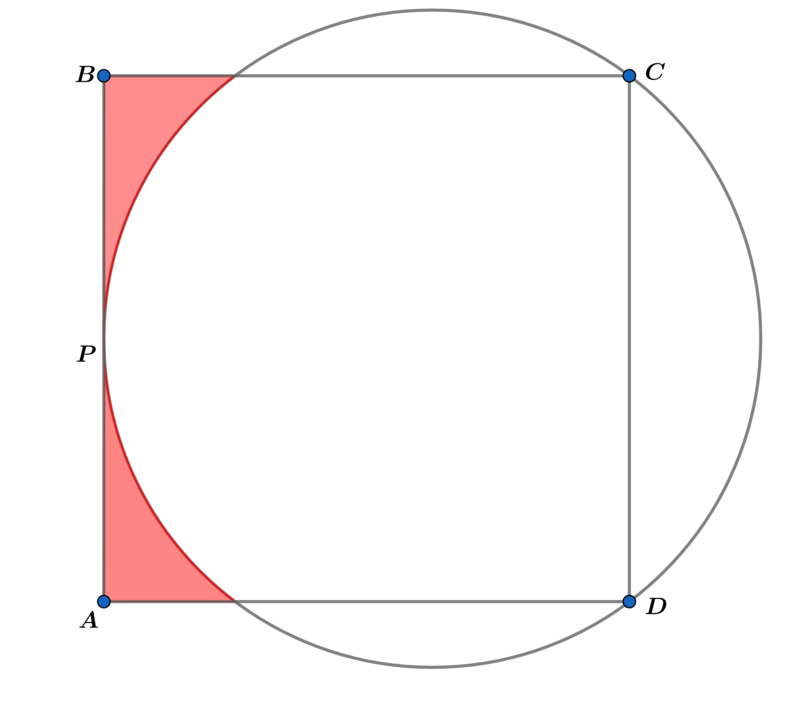
In the above diagram square A B C D is tangent to the circle at point P and vertices C and D are on the circle.
Let A R be the area of the red regions. If A A B C D A R = p α − β arcsin ( ω λ ) , where α , β , λ , ω , and p are coprime positive integers, find α + β + λ + ω + p .
The answer is 126.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice one! When you use the tangent-secant theorem (first line), I believe it should be B E ⋅ B C , not B E ⋅ B D .
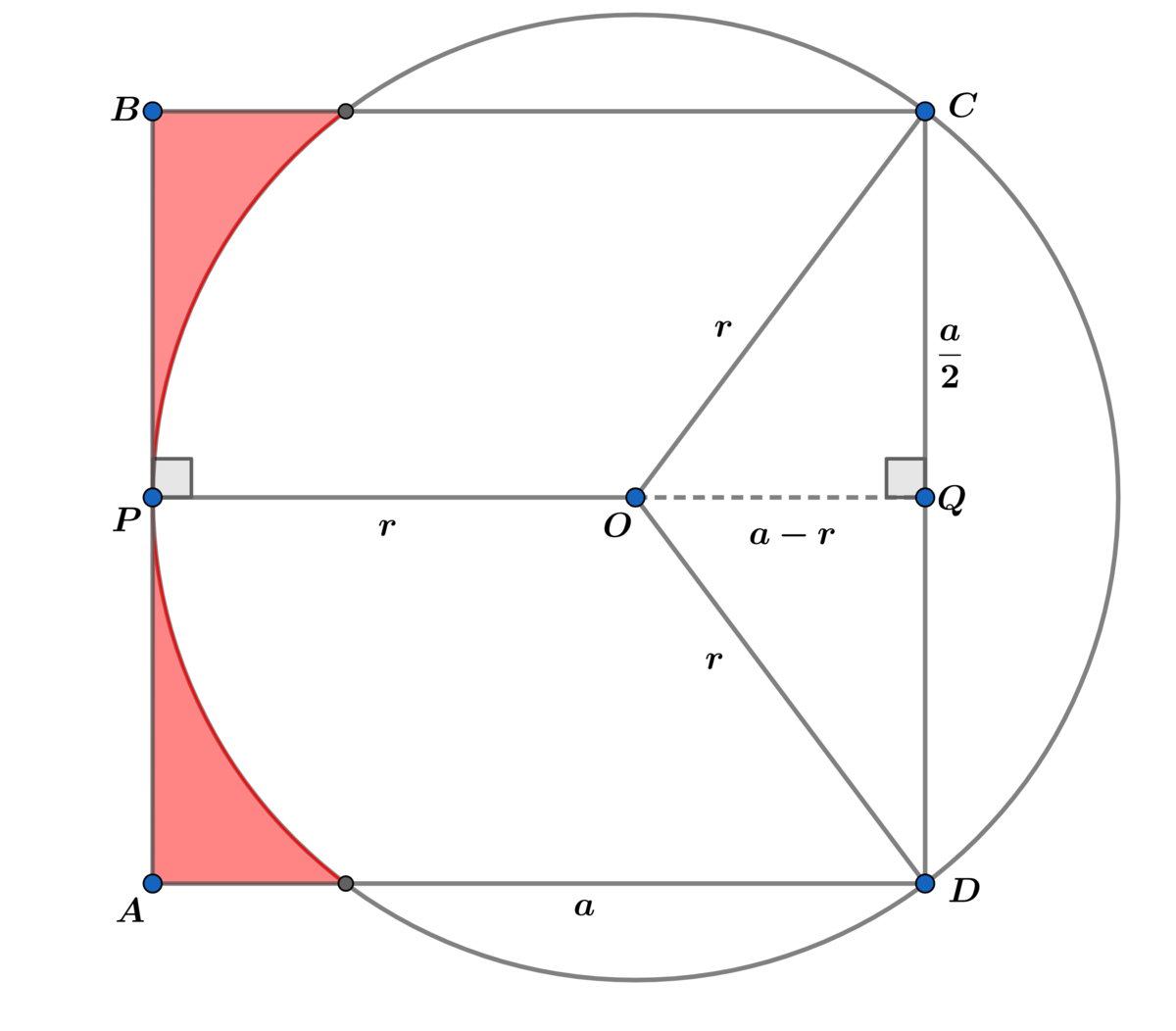
Let a be a side of square A B C D .
△ C O D is an isosceles triangle ⟹ O Q is the perpendicular bisector of base C D ⟹
C Q = Q D = 2 a
In right △ C O Q we have r 2 = a 2 − 2 a r + r 2 + 4 a 2 ⟹ a ( 5 a − 8 r ) = 0
and a = 0 ⟹ r = 8 5 a
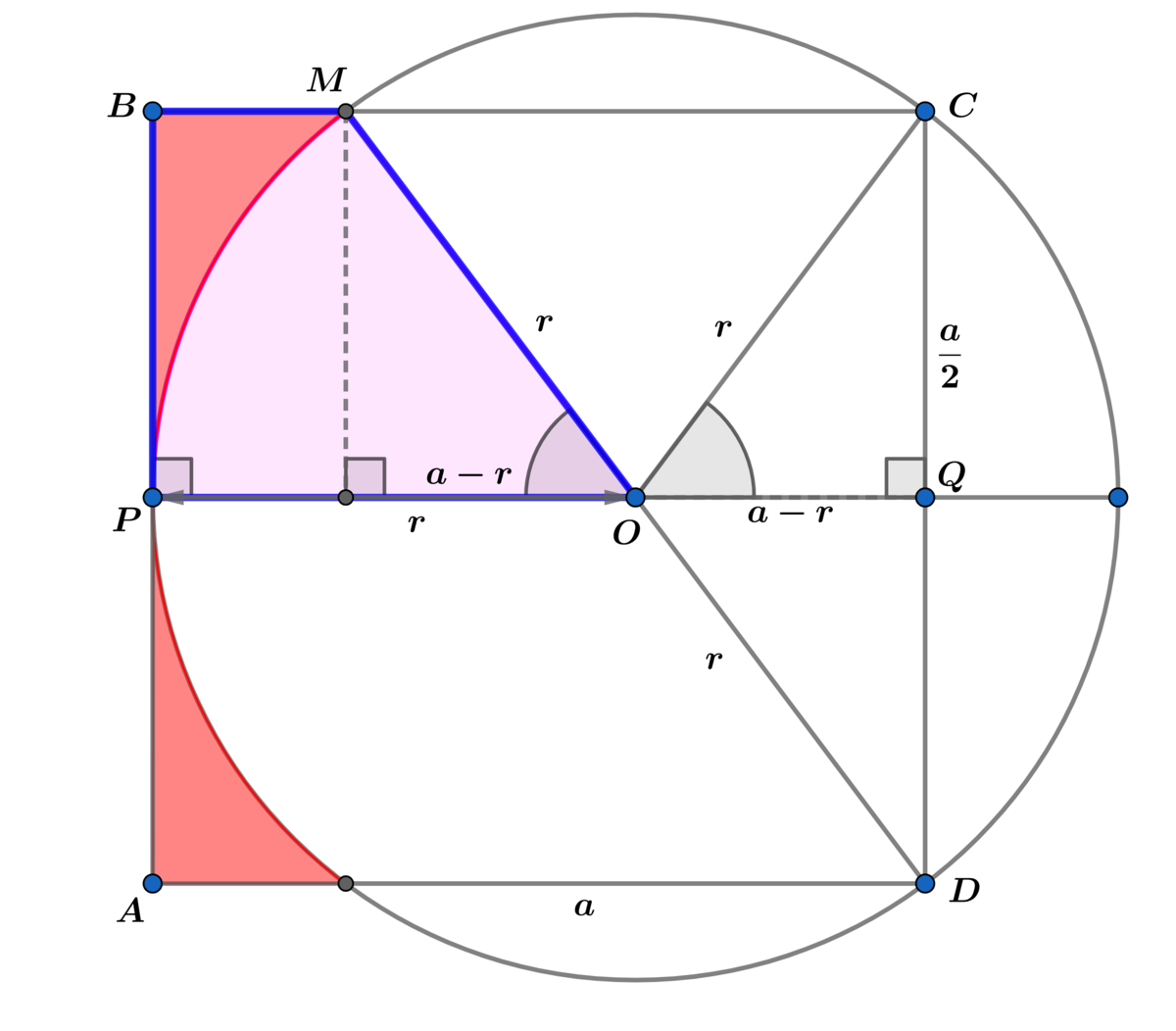
B M = a − 2 ( a − r ) = 2 r − a = 4 a and sin ( θ ) = 2 r a = 5 4 ⟹
Area of sector M O P is A s = 2 1 θ r 2 = 2 1 arcsin ( 5 4 ) ( 6 4 2 5 ) a 2 = 1 2 8 2 5 arcsin ( 5 4 ) a 2
and
Area of trapezoid P B M O is A P B M O = 2 1 ( r + B M ) ( 2 a ) = 2 1 ( 8 5 a + 4 a ) ( 2 a ) = 3 2 7 a 2
⟹ A R = 2 ( A P B M O − A s ) = 2 ( 3 2 7 − 1 2 8 2 5 arcsin ( 5 4 ) ) a 2 =
( 6 4 2 8 − 2 5 arcsin ( 5 4 ) ) a 2 ⟹ A A B C D A R = 6 4 2 8 − 2 5 arcsin ( 5 4 ) = p α − β arcsin ( ω λ )
⟹ α + β + λ + ω + p = 1 2 6 .
Let the side length of square A B C D be 1 Then the area of square A B C D , [ A B C D ] = 1 . Let B E = x . By tangent-secant theorem , we have B E ⋅ B C = B P 2 ⟹ x ⋅ 1 = ( 2 1 ) 2 ⟹ x = 4 1
Due to symmetry, we note that B E = P G = H Q = 4 1 . Since the diameter of the circle P Q = P H + H Q = 1 + 4 1 = 4 5 , the radius of the circle r = 8 5 .
Then the area of the red regions
A R = [ A B E F ] r e c t a n g l e − [ E P F G ] s e g m e n t = [ A B E F ] r e c t a n g l e − ( [ E P F O ] s e c t o r − [ E F O ] t r i a n g l e ) = A F ⋅ A B − r 2 sin − 1 ( O E E G ) + 2 1 ⋅ E F ⋅ O G = 1 ⋅ 4 1 − 8 2 5 2 sin − 1 ( 2 1 ⋅ 5 8 ) + 2 1 ⋅ 1 ⋅ ( 8 5 − 4 1 ) = 4 1 − 6 4 2 5 sin − 1 ( 5 4 ) + 1 6 3 = 6 4 2 8 − 2 5 sin − 1 ( 5 4 )
Since [ A B C D ] = 1 , [ A B C D ] A R = A R and the required answer is 2 8 + 2 5 + 4 + 5 + 6 4 = 1 2 6 .