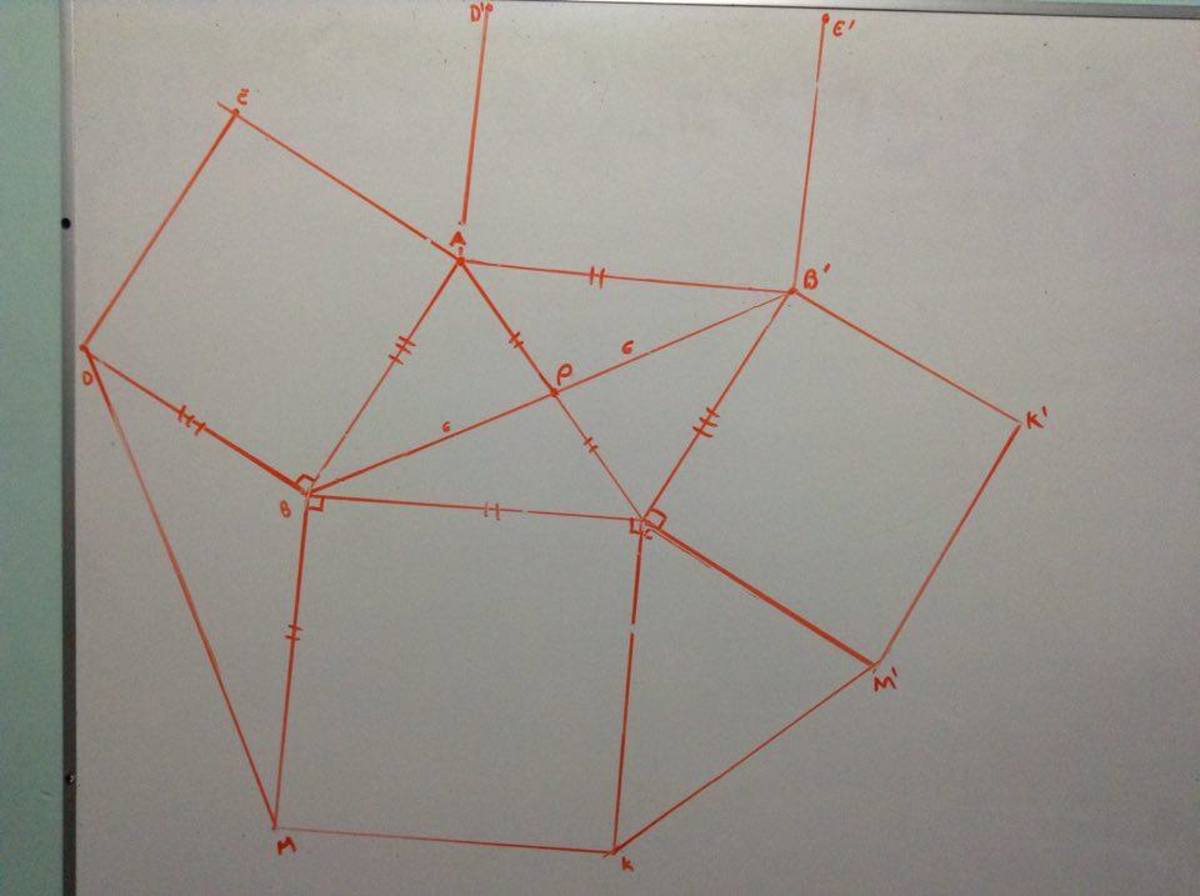
Squares and Medians

With the next figure, only extend the median $BP$ and form a parallelogram $ABCB'$ . Construct the next squares $CB'M'K'$ and $AB'E'D'$ . Given that $AB=BD=CB'$ and $BC=CK=AB'$ , then the figure $BMKM'K'B'=AEDMKC$ therefore $BB' \cong DM$ and $BB'=2BP=12 \Longrightarrow DM=12$

Hint : Setting $AB = c, BC = a, AP = CP = \dfrac{b}{2}$ and $\angle ABC = \theta$ , do the following :

1) Apply Appolonius theorem to $\Delta ABC$ to find $BP$ w.r.t. $a,b,c$ .

2) Observe that $\angle DBM = (180^{\circ} - \theta) , BD = c$ and $BM = a$ .

2) Apply cosine rule to $\Delta ABC$ and $\Delta BDM$ to find $DM$ w.r.t. $a,b,c$ .

Now, comparing expressions of $BP$ and $DM$ , we see that $\boxed{DM=2BP}$ .

P.S. There is also a Euclidean solution to this problem, and I will leave that for someone else to figure out.

Here is beautiful solution involving almost no computation:

Observe $\angle DBM = 180-\angle ABC$

Rotate $\triangle DBM$ such that $BM$ coincides with $BC$ and $ABD$ forms a straight line.

Thus $BP$ becomes the segment joining the midpoints of $AD$ and $AC$ and hence is half of $DM$

link text