Squares and midpoints
 Let
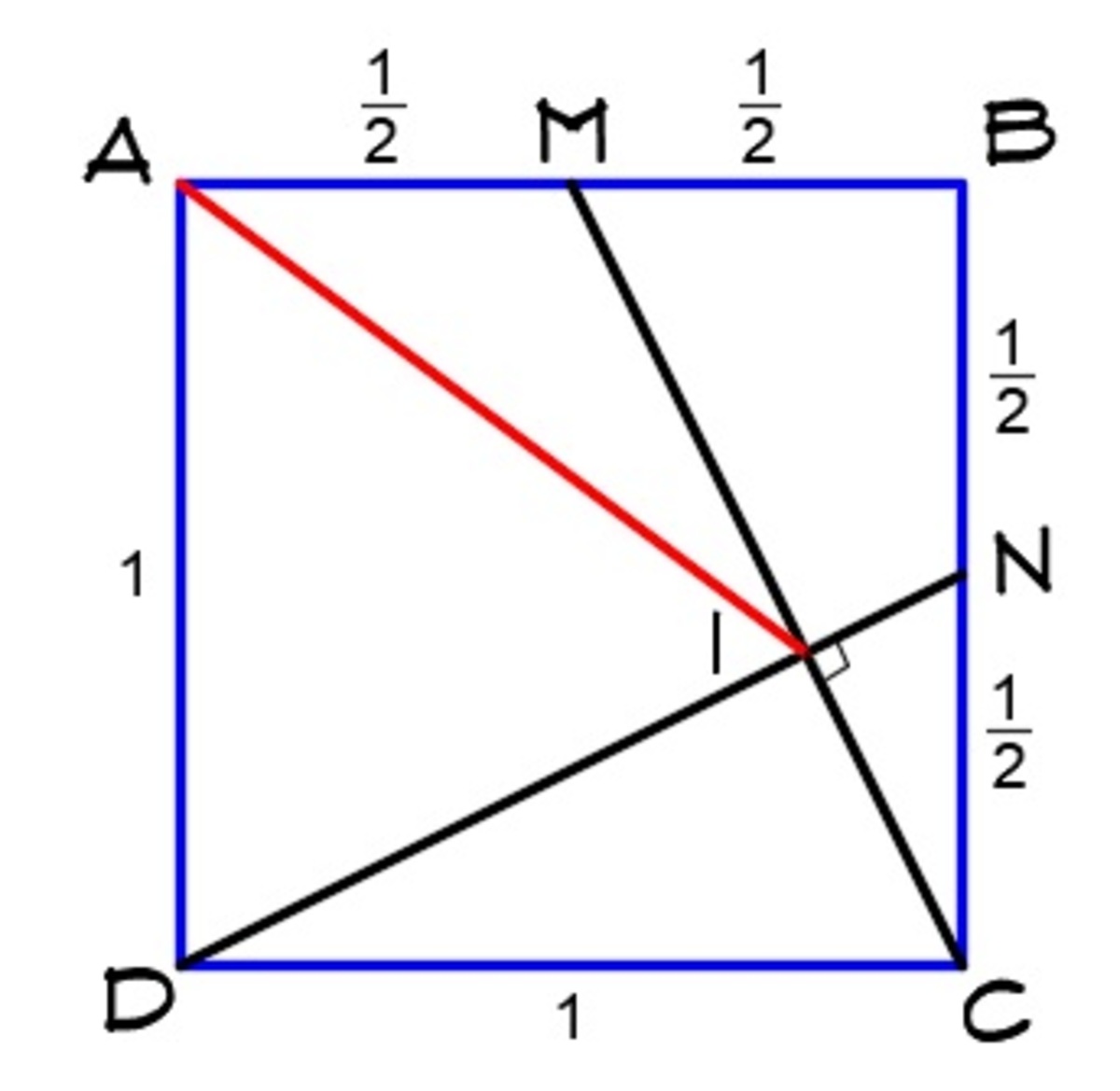
A
B
C
D
be a square with side length 1,
M
and
N
be the midpoint of line segments
A
B
and
B
C
respectively, and
C
M
and
D
N
cut at point
I
. What is the length of
A
I
?
Let
A
B
C
D
be a square with side length 1,
M
and
N
be the midpoint of line segments
A
B
and
B
C
respectively, and
C
M
and
D
N
cut at point
I
. What is the length of
A
I
?
The answer is 1.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
A grade 9 early quality test in Vietnam!
The “slope” of M C is -2 while the “slope” of N D is 2 1 , so M C ⊥ N D . This means quadrilateral A M I D is cyclic, since both ∠ M A D and ∠ M I D are both right. Using congruent triangles △ A M D ≅ △ B M C and properties of cyclic quadrilaterals, we have
∠ A D I = 1 8 0 ∘ − ∠ A M I = ∠ B M I = ∠ A M D = ∠ A I D .
Thus, △ A I D is isosceles, giving us A I = A D = 1 .
 By pythagorean theorem,
M
C
=
1
2
+
(
2
1
)
2
=
4
5
=
2
1
5
.
By pythagorean theorem,
M
C
=
1
2
+
(
2
1
)
2
=
4
5
=
2
1
5
.
Since △ N I C ∼ △ M B C , we have
N C I C = M C B C ⟹ 2 1 I C = 2 1 5 1 ⟹ I C = 5 1 = 5 5
Then: M I = M C − I C = 2 1 5 − 5 1 5 = 1 0 3 5
And: tan ∠ B M C = B M B C = 2 1 1 = 2 ⟹ ∠ B M C = tan − 1 2
It follows that: ∠ A M C = 1 8 0 − ∠ B M C = 1 8 0 − tan − 1
Apply cosine rule on △ A M I , we have
( A I ) 2 = ( A M ) 2 + ( M I ) 2 − 2 ( A M ) ( M I ) cos ∠ A M C = ( 2 1 ) 2 + ( 1 0 3 5 ) 2 − 2 ( 2 1 ) ( 1 0 3 5 ) [ cos ( 1 8 0 − tan − 1 2 ) ] = 1
Finally, A I = ( A I ) 2 = 1 = 1
It's actually not that complicated. This is a grade 8 problem in our country. Remember this: The median of a right triangle, starting from the right angle to the hypotenuse, is equal to 1/2 of the hypotenuse.
Use coordinate geometry with D(0,0). Equation of line DN is y=0.5x, MC: y=-2x + 2. I is intersection point of line DN and MC. So we can find its coordinate I(4/5,2/5). So by distance formula we can find AI = 1
We can easily prove that △ B M C ≅ △ C N D ( S A S ) and therefore C M ⊥ D N and ∠ M I D = 9 0 ∘ .
Let C M cut A D at E . We can also easily prove that △ B M C ≅ △ A M E ( A S A ) and therefore A is the midpoint of D E . On the other hand, △ D I E is a right triangle at I and its median, I A , starts from the right angle. We can conclude that A I = 2 1 D E = A D = 1