Squares in a semicircle
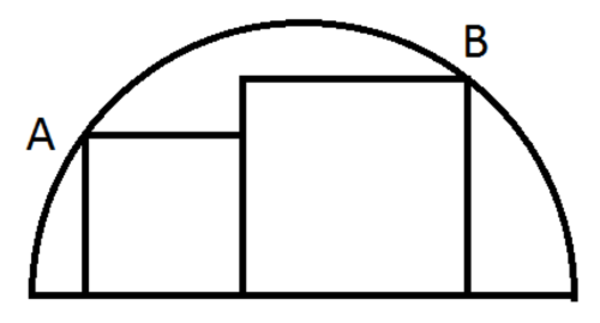
Points and lie on a semicircle of radius . What is the total area of the two squares underwritten in the circle?
The answer is 49.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
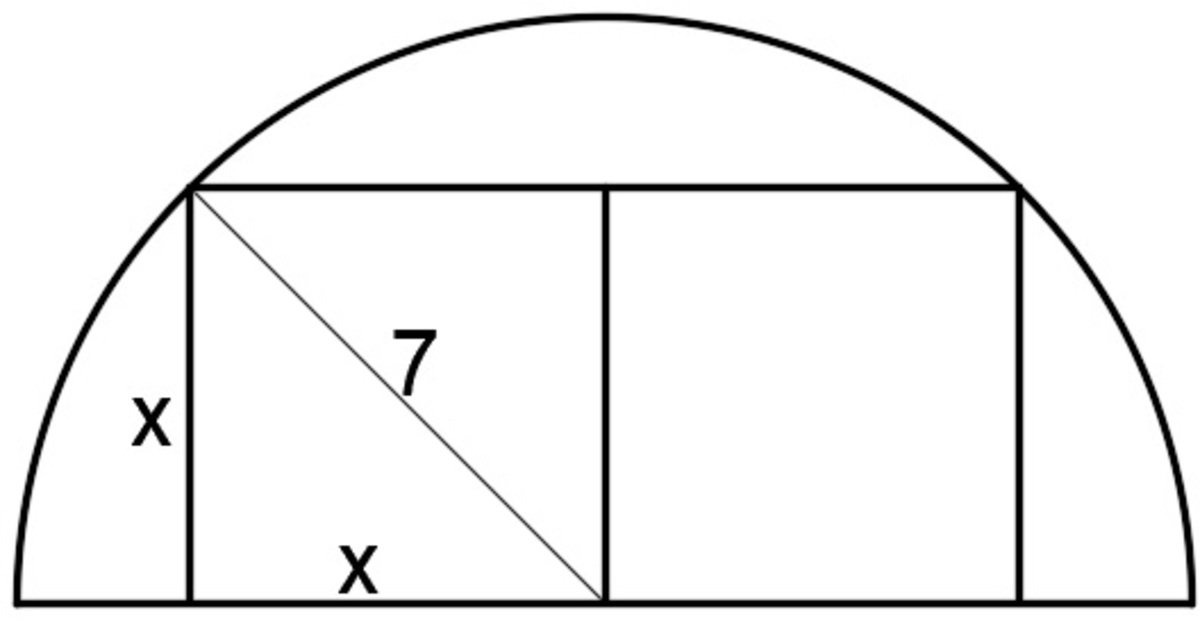
The squares have side lengths between 0 and 7 . Call the sides 7 sin θ and 7 sin γ , for θ , γ ∈ [ 0 , π / 2 ] . Then the left square has height 7 sin θ and so point A is ( − 7 cos θ , 7 sin θ ) . Similarly point B is ( 7 cos γ , 7 sin γ ) . The difference between the x -coordinates is the sum of the lengths of the two squares, so 7 cos θ + 7 cos γ = 7 sin θ + 7 sin γ .
Using addition formulas, we get 1 4 cos ( 2 θ + γ ) cos ( 2 θ − γ ) = 1 4 sin ( 2 θ + γ ) cos ( 2 θ − γ ) , so cos ( 2 θ + γ ) = sin ( 2 θ + γ ) , which means that θ + γ = π / 2 . That is, sin θ = cos γ and cos θ = sin γ (which makes it clear that the original equation is satisfied).
The sum of the areas of the squares is 4 9 sin 2 θ + 4 9 sin 2 γ = 4 9 sin 2 θ + 4 9 cos 2 θ = 4 9 .