Squares inside circle
Geometry
Level
3
In The given figure, what is the value of the Radius
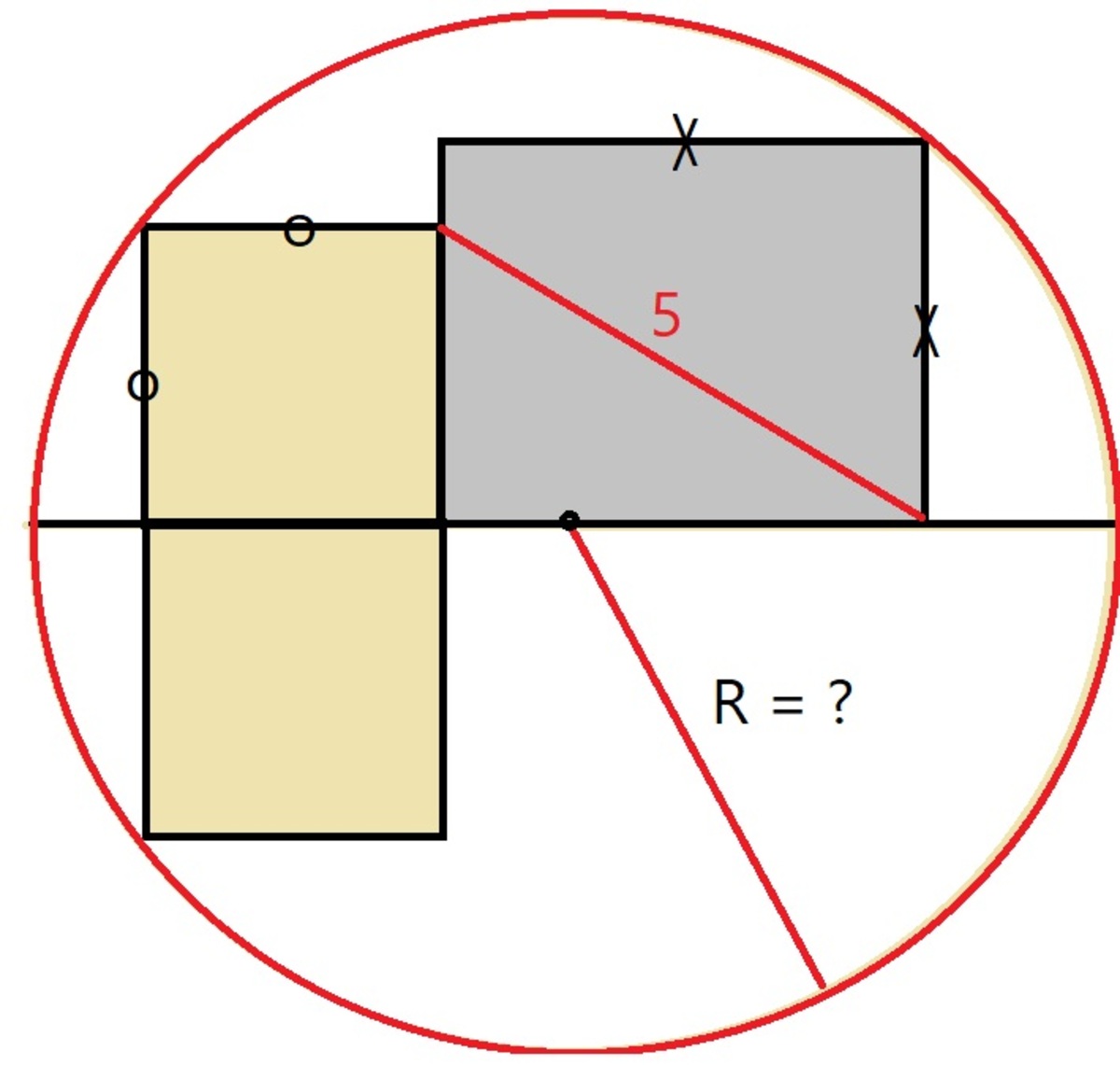
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Label the diagram as follows, and let the side of the square on the left be a , let the side of the square on the right be b , and let D H = x .
Then by the Pythagorean Theorem from △ D C G we have a 2 + b 2 = 2 5 , from △ A B H we have a 2 + ( a + x ) 2 = R 2 , and from △ G H F we have b 2 + ( b − x ) 2 = R 2 .
Then R 2 = a 2 + ( a + x ) 2 = b 2 + ( b − x ) 2 , which solves to x = b − a (for positive values of a and b ).
Substituting x = b − a into a 2 + ( a + x ) 2 = R 2 gives a 2 + b 2 = R 2 , and since a 2 + b 2 = 2 5 we have a 2 + b 2 = R 2 = 2 5 , which solves to R = 5 .