Squares, triangles... and a circumference!
Geometry
Level
3
-
A square
is inscribed in a circumference.
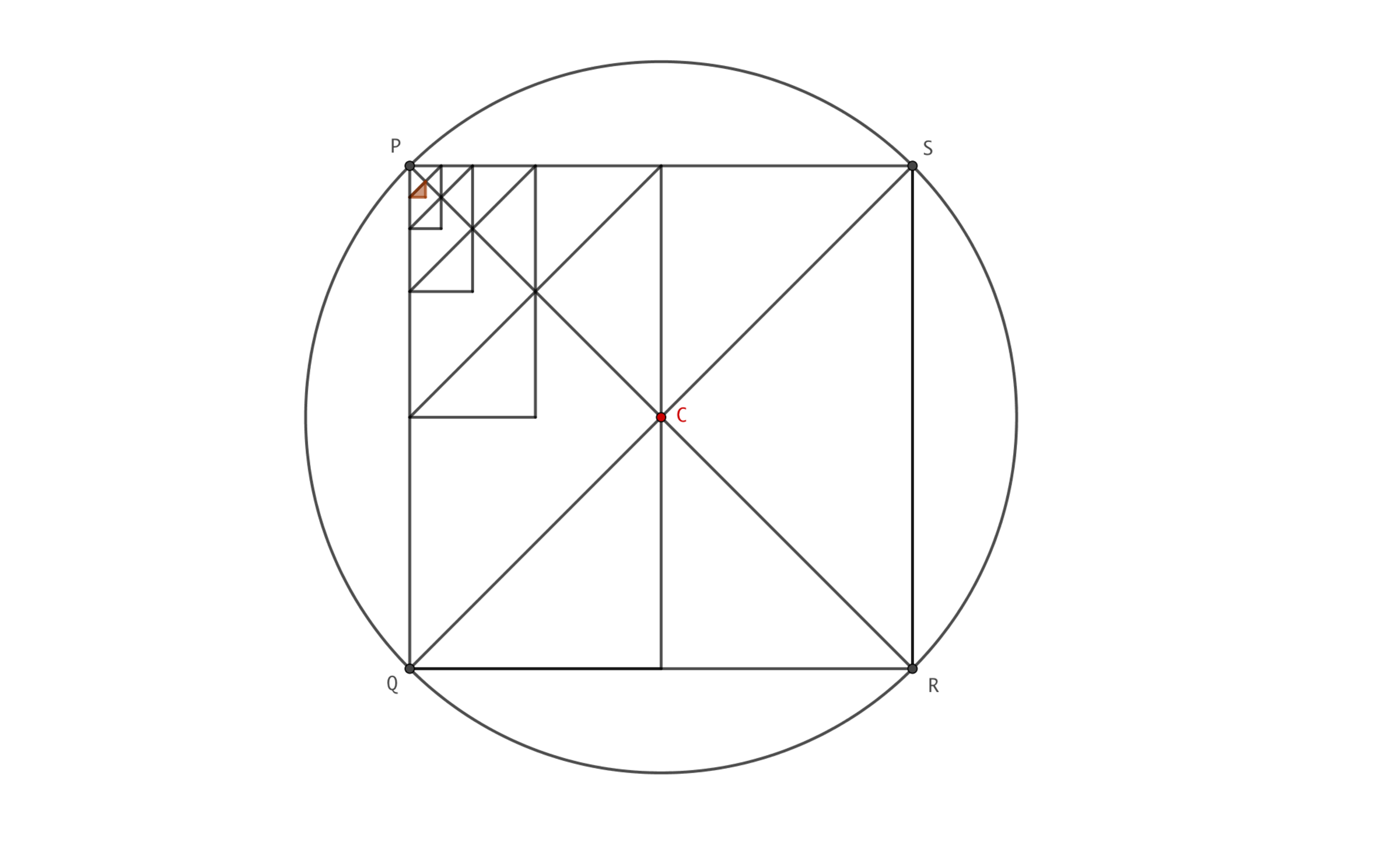
- Find the AREA of the RED TRIANGLE, rounding it to the SECOND decimal figure.
- The measure of the length of the circumference is .
- is the center of the circumference.
The answer is 0.22.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
From the circumference it's easily deducted that the radius of the circle is 2 2 2 . Making use of a 45-45-90 triangle this leads to the side lengths of the triangle, down left of the square. The lengths are 1 1 1 . So the are is 55.5. Now the red triangle has side 4 times as small(its halved 4 times), so the area is ( 1 6 1 ) 4 as small. So the area is 0.22