Squares + Triangles!
Figure 1:-
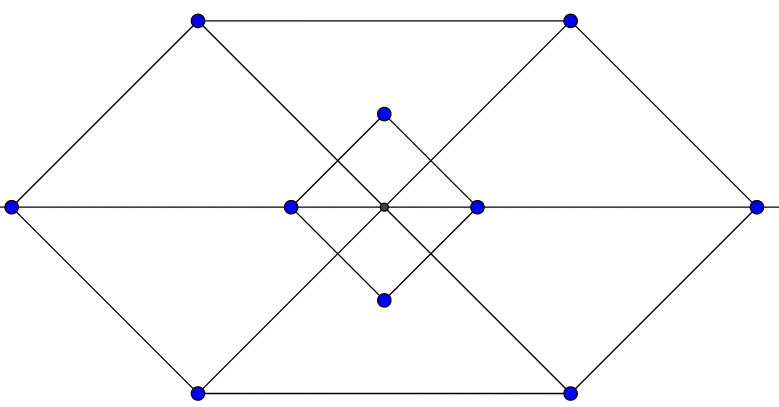
Figure 2:-
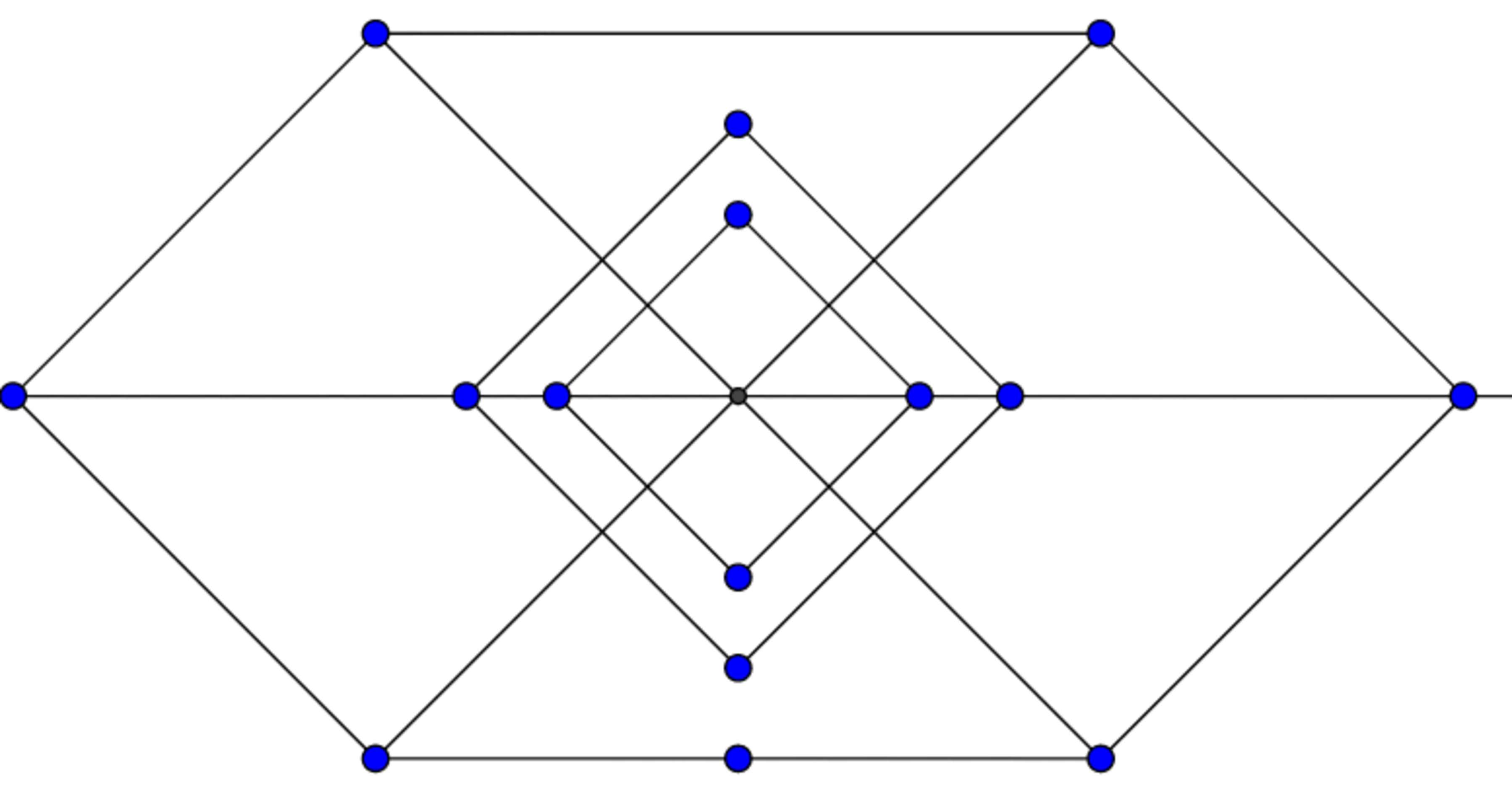
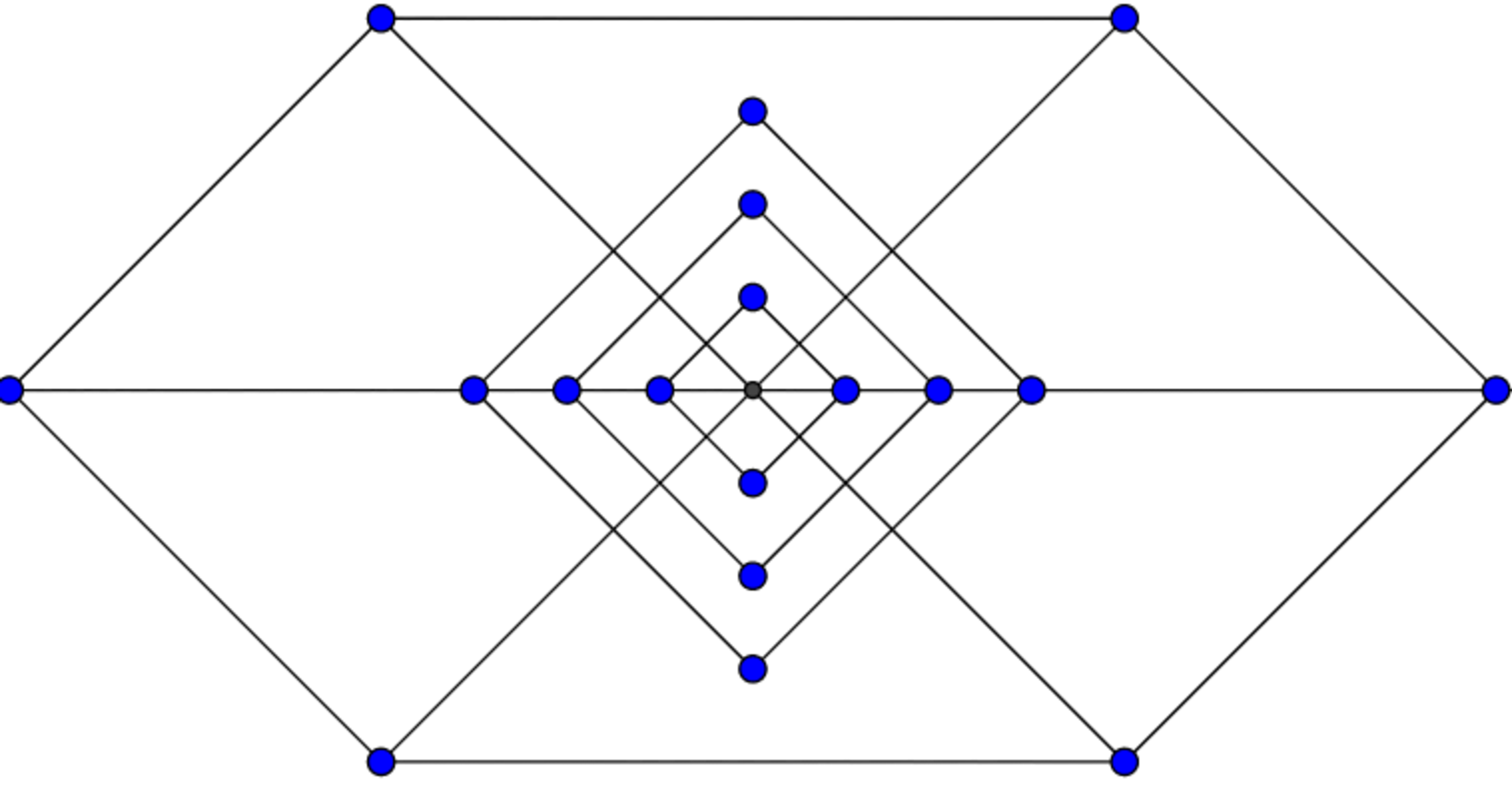
Figure 3:-
Find the total number of quadrilaterals in the figure that follows this pattern.
Clarification:- The squares with common centre are always within the big hexagon. The sides and edges of these squares can in no case touch or intersect the sides of the big hexagon.
The answer is 8148672.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In figure 1, there are 1 2 quadrilaterals.
In figure 2, there are 2 8 quadrilaterals.
In figure 3, there are 4 8 quadrilaterals.
(For more clarification):-
In figure 4, there are 7 2 quadrilaterals.
In figure 5, there are 1 0 0 quadrilaterals.
So, we observe that in the n th figure, the number of quadrilaterals is found by the formula:-
1 2 n + ( 4 × n = 1 ∑ n ( n − 1 ) )
∴ In the 2 0 1 6 th figure that follows this pattern, there would be:-
( 1 2 × 2 0 1 6 ) + ( 4 × n = 1 ∑ 2 0 1 6 ( n − 1 ) )
= ( 1 2 × 2 0 1 6 ) + ( 4 × 2 2 0 1 5 × 2 0 1 6 )
= ( 1 2 × 2 0 1 6 ) + ( 2 0 1 6 × 4 0 3 0 )
= ( 2 0 1 6 × 4 0 4 2 )
= 8148672 quadrilaterals. □