Squares within squares
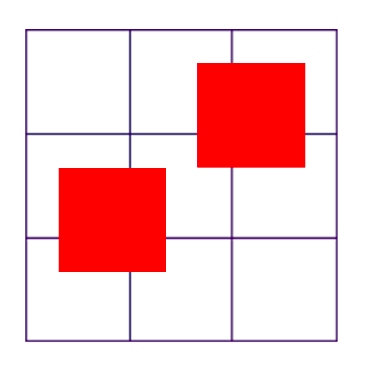 Consider a
grid of
squares. Now consider two other grid-squares, the same size as the previous ones, being placed randomly on the
grid. The squares must be entirely on the grid, are allowed to overlap over the interior grid lines, and must have each side of the square parallel to a grid line. If the chance that the squares do not overlap is
for coprime positive integers
and
, find
.
Consider a
grid of
squares. Now consider two other grid-squares, the same size as the previous ones, being placed randomly on the
grid. The squares must be entirely on the grid, are allowed to overlap over the interior grid lines, and must have each side of the square parallel to a grid line. If the chance that the squares do not overlap is
for coprime positive integers
and
, find
.
The answer is 23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For the two squares to overlap, the x and y coordinates of their centers must separately be both within one of each other. P(x coordinates being within one of each other) = 3/4, P(y coordinates being within one of each other) = 3/4, P(The two squares overlapping) = 9/16, P(The squares not overlapping) = 7/16, a = 7, b = 16, a + b = 23