Squares within Squares
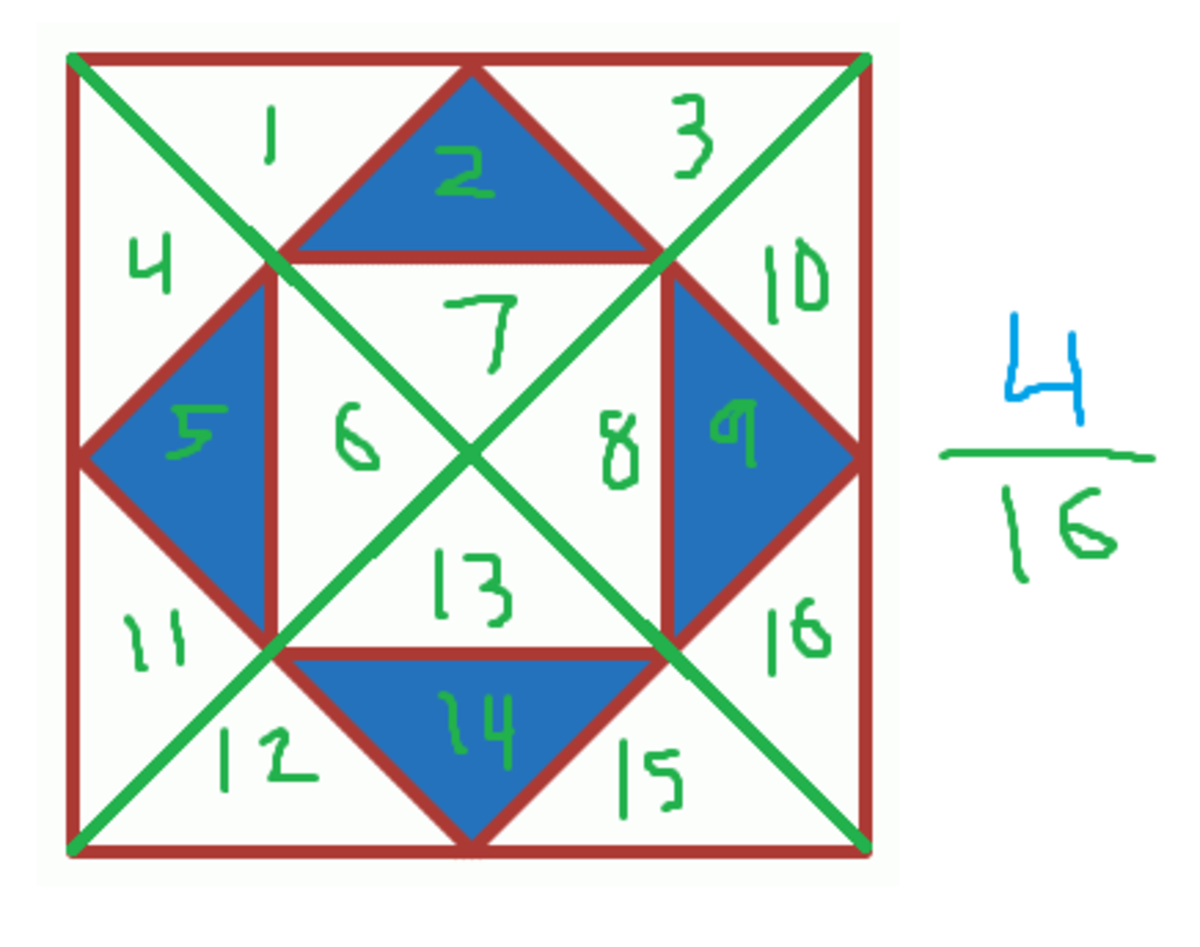
 The diagram above depicts a square in a square inside another square. What fraction of the largest square is shaded blue?
The diagram above depicts a square in a square inside another square. What fraction of the largest square is shaded blue?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Nice method to explain
Much simpler than my method! Wish I'd thought about that!
Let's put half length of the largest square as= x
Using Pythagoras theorem, length of the medium square = sqrt(x^2+x^2)= sqrt(2x^2)
We can rearrange the 4 triangles into a rectangle
Area of rectangle = (sqrt(2x^2))(0.5sqrt(2x^2)) = x^2
Area of largest square = 2x(2x) = 4x^2
Fraction shaded = (x^2)/4x^2 = 1/4
Is there a more direct way of seeing that the triangles give us x^2? Think about flipping them.
If a is the side length of largest square then its area is a 2 and area of middle square will be 2 1 × a 2 ( ∵ a i s t h e d i a g o n a l o f m i d d l e s q u a r e ) = 2 a r e a o f l a r g e s t s q u a r e .
Similarly area of smallest square = 2 a r e a o f m i d d l e s q u a r e = 4 a r e a o f l a r g e s t s q u a r e .
So, area of shaded portion = 2 1 − 4 1 = 4 1 .
You don't know that
Assume the smallest square has a side of 1 unit. Its area is 1 u n i t 2 .
Since they are squares enclosed within each other, we can say they are 4 5 − 4 5 − 9 0 triangles.
Thus using the 4 5 − 4 5 − 9 0 rule, we can say that ONE SIDE OF THE BLUE TRIANGLE = 2 ( 2 ) × 1
Thus one whole side of the blue triangle = 2 ( 2 ) × 2 = > ( 2 )
The area of the blue triangle is then = ( 2 ) 2 = > 2 u n i t s 2
Using the same angle property, we can say that the side of the biggest triangle is 2 ( 2 ) × ( 2 ) = 2 2 = > 1
One whole side is then 2 × 1 = 2
The area of the biggest square is 2 2 = 4 u n i t s 2 Thus, 2 u n i t s 2 − 1 u n i t 2 , out of 4 u n i t s 2 gives 4 1 // This is my first answer, do tell me how I can improve it :)
I solved it the same
An inner square included in an outer square through the mid points of its sides, then the inner square has half the area of the outer square. Consider 4X to be the area of the first square. Second square has an area of 2X. Third square has an area of X. To get the area of shaded part 2X-X = X. Which is obviously 1/4th of 4X.
The blue square is one half of the big square. We know this because the sum of all outer triangles equals the blue square. That is one half. The small white square is half of the blue square, as the same reasoning can be applied. That makes the blue shaded area one fourth of the big square.
Nice approach, using it iteratively.