Squaring a circle, again

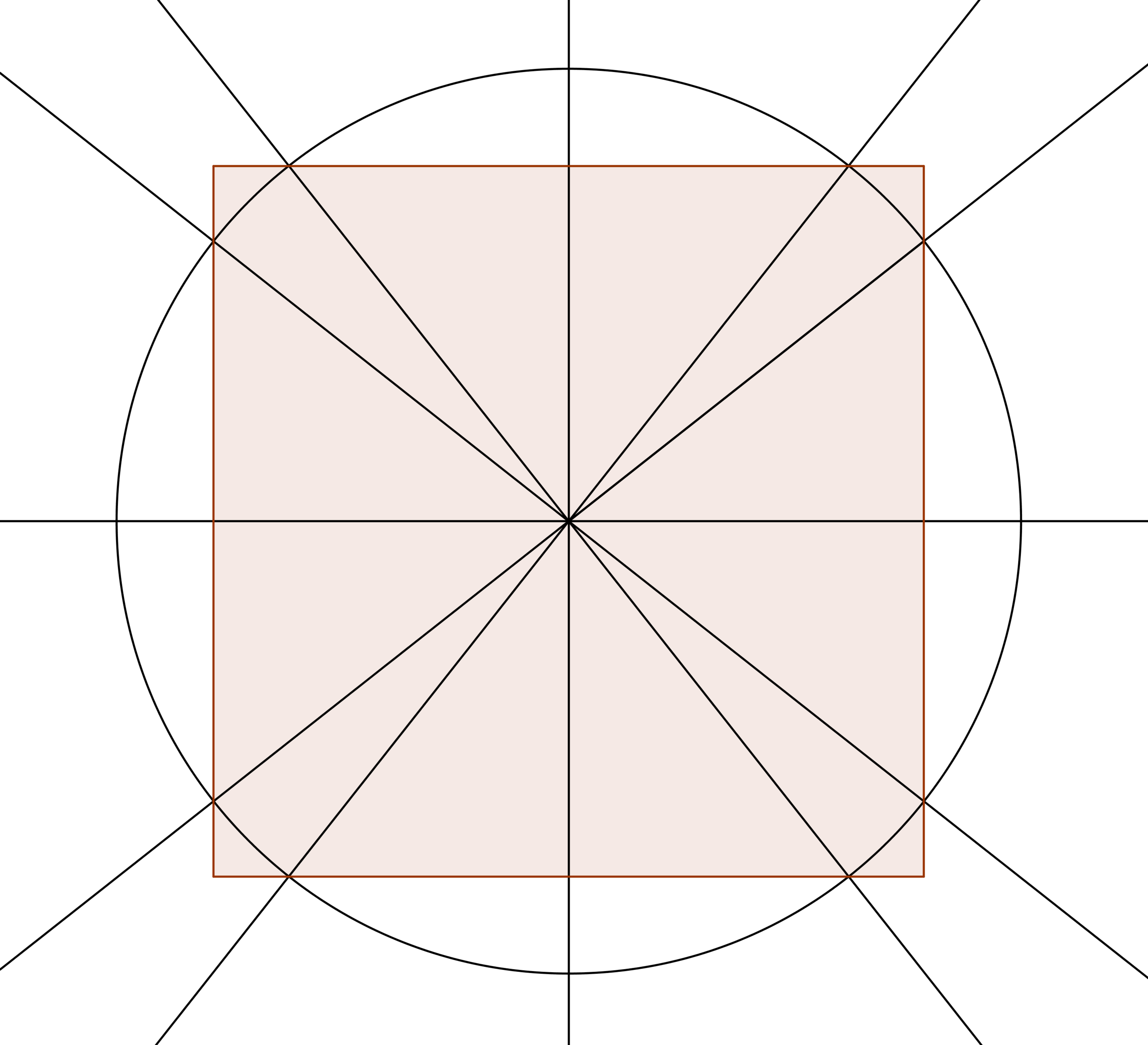
There is a unit circle with its center point at $(0,0)$ . There is a set of 4 linear functions in the form: $\dfrac{m}{n} x , -\dfrac{m}{n} x , \dfrac{n}{m} x , -\dfrac{n}{m} x$ which intersect the circle at 8 points. There is a square that intersects the unit circle at the same 8 points with sides parallel to X and Y axis.
If $s$ is semi-perimeter of the square then $\lfloor { s \times 10^9 } \rfloor = \lfloor {\pi \times 10^9 } \rfloor$ .

Find the set of smallest positive integer numbers $m < n$ such that they meet the described criteria. Find all the prime factors of numbers $m$ and $n$ . For each factor $p_{i}$ , find $s_{i}$ which is number of primes equal to or less then $p_{i}$ . Give answer as a product of all $s_{i}$ .

Details and Assumptions:

If some prime number appears more than once as a factor use it only once in the solution, i.e. if $m$ has prime factors: $2^2, 3, 5$ and $n$ has prime factors: $2^3, 5^2, 7$ , use only numbers $2, 3, 5, 7$ in calculating the final answer which in this case would be $1\times 2\times 3 \times 4 = 24$ . The problem is original.