Squaring is important. :D

Algebra Level 3

Evaluate:

$(23+4\sqrt{19})^{3/2} - (23-4\sqrt{19})^{3/2}$ .

The answer is 244.

2 solutions

Jaiveer Shekhawat
Oct 27, 2014

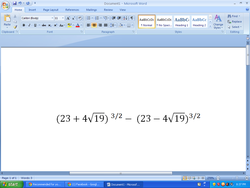
According to my view, the question should have positive sign between the two expressions rather than a negative sign if we want to get the answer as 244 because...

if there was a negative sign then the answer wouldn't have been an integer!!

You have a wrong approach. (2+√19)^2 ≠ (23+4√19) ...

Christian Daang - 6 years, 7 months ago

I think, there's something Wrong about your solution.

Christian Daang - 6 years, 7 months ago

Christian Daang
Oct 27, 2014

Let a = 23 and b = 4√19

Then, let x = that expression:

(a+b)^(3/2) - (a-b)^(3/2) = x

square the both side:

(a+b)^3 - 2[(a+b)(a-b)]^(3/2) + (a-b)^3 = x^2

a^3 + 3ba^2 + 3ab^2 + b^3 - 2[(a^2) - (b^2)]^(3/2) + a^3 - 3ba^2 + 3ab^2 - b^3 = x^2

2a^3 + 6ab^2 - 2[a^2 - b^2]^(3/2) = x^2

√{2a^3 + 6ab^2 - 2[a^2 - b^2]^(3/2)} = x

√{2(23)^3 + 6(23)(4√19)^2 - 2[(23)^2 - (4√19)^2]^(3/2)} = x

√{24334 + 41952 - 2[225]^(3/2)} = x

√{66286 - 2[3375]} = x

√59536 = x

244 = x

Final Answer: 244.

Squaring is important. :D

The answer is 244.

2 solutions

0 pending reports