Squaring the pentagon?
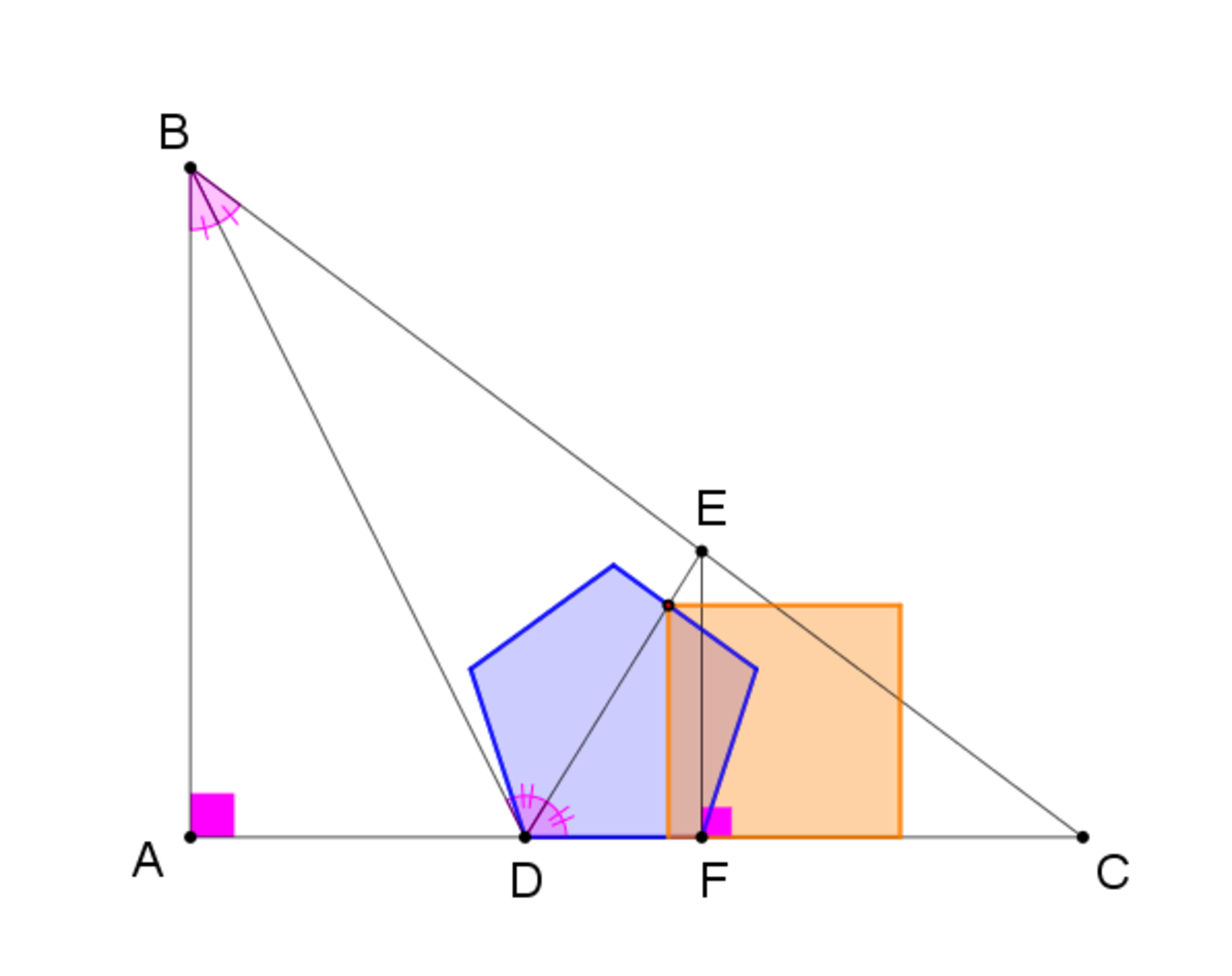
△ A B C is a right triangle with side lengths A B = 3 , A C = 4 , and B C = 5 . B D and D E are the angle bisectors of ∠ A B C and ∠ B D C respectively. E F is perpendicular to A C . The blue polygon is a regular pentagon of side D F and the orange one is a square with one side on A C and one vertex being the intersection of D E with a side of the pentagon.
Which of these two polygons has a greater area, the square or the pentagon?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The shortest, therefore the best solution!
Let the top vertex of the pentagon be G and the top left vertex of the square be H . Place the whole diagram on a coordinate plane so that A is at A ( 0 , 0 ) , B is at B ( 0 , 3 ) , and C is at C ( 4 , 0 ) .
Then B C is on the line through B ( 0 , 3 ) and C ( 4 , 0 ) , which is y = − 4 3 x + 3 .
Since B D bisects ∠ A B C , A D = 3 tan ( 2 1 tan − 1 3 4 ) = 2 3 , so D is at D ( 2 3 , 0 ) .
Since D E bisects ∠ B D C , tan ∠ E D F = tan 2 1 ∠ B D C = tan 2 1 ( 1 8 0 ° − ∠ B D A ) = cot ( 2 1 ∠ B D A ) = cot ( 2 1 tan − 1 2 ) = 2 1 ( 1 + 5 ) = ϕ , so D E is on the line y = ϕ ( x − 2 3 ) .
E is at the intersection of B C and D E , or y = − 4 3 x + 3 and y = ϕ ( x − 2 3 ) , which solves to E ( 9 − 3 5 , 4 1 ( 9 5 − 1 5 ) ) .
The side of the pentagon is D F = 9 − 3 5 − 2 3 = 2 1 ( 1 5 − 6 5 ) , so its area is A pentagon = 4 1 5 ( 5 + 2 5 ( 2 1 ( 1 5 − 6 5 ) ) 2 ≈ 1 . 0 7 8 6 .
The height of the pentagon is 2 1 5 + 2 5 ⋅ 2 1 ( 1 5 − 6 5 ) = 4 3 5 ( 5 − 2 5 ) and the midpoint of D F is ( 2 1 ( 2 3 + 9 − 3 5 ) , 2 1 ( 0 + 0 ) ) = ( 4 1 ( 2 1 − 6 5 ) , 0 ) , so G is at G ( 4 1 ( 2 1 − 6 5 ) , 4 3 5 ( 5 − 2 5 ) ) .
By the properties of a regular pentagon, the slope of G H is − tan 3 6 ° = − 5 − 2 5 , and since it is through G ( 4 1 ( 2 1 − 6 5 ) , 4 3 5 ( 5 − 2 5 ) ) , it is on the line y = − 5 − 2 5 ( x − 4 1 ( 2 1 − 6 5 ) ) + 4 3 5 ( 5 − 2 5 ) .
H is at the intersection of G H and D E , or y = − 5 − 2 5 ( x − 4 1 ( 2 1 − 6 5 ) ) + 4 3 5 ( 5 − 2 5 ) and y = ϕ ( x − 2 3 ) , which solves to a y -coordinate of 1 + 5 + 2 5 − 2 5 3 5 ( 5 − 2 5 ) , so the area of the square is A square = ( 1 + 5 + 2 5 − 2 5 3 5 ( 5 − 2 5 ) ) 2 ≈ 1 . 0 8 0 3 .
Therefore, the square has a larger area than the pentagon.
Here is a (lengthy) solution, which avoids coordinate geometry. First we prove the
Lemma :
Figure 1 In figure 1, let a , b , c , x and y be the lengths of the line segments B C , C A , A B , B D and D C respectively, with A D being the bisector of A .
Then, the following relations hold x = b + c a c and y = b + c a b Proof
By the angle bisector theorem , y x = b c ⇒ a − x x = b c ⇒ x b = c ( a − x ) ⇒ x b = c a − c x ⇒ x b + x c = a c ⇒ x = b + c a c Similar proof for y = b + c a b .
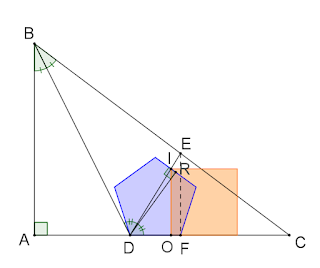 Figure 2
Applying the lemma on
△
A
B
C
we have
A
D
=
B
A
⋅
B
C
A
C
⋅
B
A
=
3
+
5
4
⋅
3
⇒
A
D
=
2
3
Easily,
D
C
=
A
C
−
A
D
=
4
−
2
3
⇒
D
C
=
2
5
.
Figure 2
Applying the lemma on
△
A
B
C
we have
A
D
=
B
A
⋅
B
C
A
C
⋅
B
A
=
3
+
5
4
⋅
3
⇒
A
D
=
2
3
Easily,
D
C
=
A
C
−
A
D
=
4
−
2
3
⇒
D
C
=
2
5
.
Moreover, by the angle bisector theorem,
B
D
2
=
B
A
⋅
B
C
−
A
D
⋅
D
C
=
3
⋅
5
−
2
3
⋅
2
5
⇒
B
D
=
2
3
5
(Pythagoras’ theorem on
△
A
B
D
could have been used as well.)
Now, we focus on
△
B
D
C
.
Using the lemma we find
E
C
:
E
C
=
B
D
+
D
C
B
C
⋅
D
C
=
2
3
5
+
2
5
5
⋅
2
5
⇒
E
C
=
4
5
(
3
5
−
5
)
Then, the angle bisector theorem gives
D
E
2
=
B
D
⋅
D
C
−
B
E
⋅
E
C
=
2
3
5
⋅
2
5
−
(
5
−
4
5
(
3
5
−
5
)
)
⋅
4
5
(
3
5
−
5
)
⇒
D
E
=
4
3
2
5
0
−
1
1
0
5
Triangles
△
E
F
C
and
△
B
A
C
are similar, thus,
A
B
E
F
=
B
C
E
C
⇒
E
F
=
B
C
A
B
⋅
E
C
=
5
3
⋅
4
5
(
3
5
−
5
)
⇔
E
F
=
4
3
(
3
5
−
5
)
Hence,
sin
(
∠
E
D
F
)
=
D
E
E
F
=
4
3
2
5
0
−
1
1
0
5
4
3
(
3
5
−
5
)
=
1
0
1
(
5
+
5
)
For the comparison of the areas of the two polygons and in order to simplify the calculations needed, we change the scale, setting the side of the pentagon to be of unit length, i.e. D F = 1 .
Then for the area of the pentagon
A
5
=
4
2
5
+
1
0
5
D
F
=
4
2
5
+
1
0
5
⋅
1
⇒
A
5
≈
1
.
7
2
0
Let
D
R
be perpendicular to one side of the pentagon,
I
be the upper left vertex of the square and
θ
=
∠
I
D
R
, as seen in figure 2.
Then
D
R
is the height of the pentagon, hence
D
R
=
2
1
5
+
2
5
⋅
D
F
⇒
D
R
=
2
1
5
+
2
5
.
Moreover,
∠
F
D
R
is half the angle of the pentagon, hence
∠
F
D
R
=
1
0
3
π
.
For the area of the square,
A 4 = I O 2 = ( D I ⋅ sin ( ∠ I D F ) ) 2 = ( cos θ D R ⋅ sin ( ∠ E D F ) ) 2 = cos 2 ( s i n − 1 1 0 1 ( 5 + 5 ) − 1 0 3 π ) 4 5 + 2 5 ⋅ 1 0 1 ( 5 + 5 ) ⇒ A 4 ≈ 1 . 7 2 3
Comparing the two areas we see that the square has a greater area.
We need to find the measure of ∠ E D F = θ . But first let us find the measure of 2 1 ∠ B ) :
1 − tan 2 2 B 2 tan 2 B 2 tan 2 2 B + 3 tan 2 B − 2 ⟹ tan 2 B tan ∠ B D A tan ∠ B D C ⟹ 1 − tan 2 θ 2 tan θ tan 2 θ − tan θ − 1 ⟹ tan θ = tan B = 3 4 = 0 = 2 1 = 2 = − 2 = − 2 = 0 = φ = 2 1 + 5 the golden ratio
Now consider the sizes of the pentagon and square. Let the radius of the pentagon be 1 and its height h = 1 + cos 3 6 ∘ and its area A 5 = 2 5 sin 7 2 ∘ ≈ 2 . 3 7 7 6 4 1 2 9 1 . Let the side length of the square be a and its left side is a distance b from the central axis of the pentagon. Then at the bases of the pentagon and square a cot θ = sin 3 6 ∘ + b ⟹ b = a cot θ − sin 3 6 ∘ and the height of the pentagon:
b tan 3 6 ∘ + a ( a cot θ − sin 3 6 ∘ ) tan 3 6 ∘ + a ⟹ a ⟹ A □ = a 2 = h = 1 + cos 3 6 ∘ = 1 + cot θ tan 3 6 ∘ 1 + cos 3 6 ∘ + sin 3 6 ∘ tan 3 6 ∘ ≈ 1 . 5 4 3 1 5 0 3 1 4 ≈ 2 . 3 8 1 3 1 2 8 9 3
Therefore, the area of square A □ > A p .