Squeegees

Sorry for the inconsistent image size; it would have been tiresome to copy and edit the TeX into the solutions box.

Placing the window in the cartesian plane, with the bottom left corner ar (0,0), at any given time, the squeegee makes an angle $\theta$ with the horizontal, that goes from $\frac{\pi}{2}$ to $0$ , If you consider a new sqeegee at angle $\theta'=\theta+h$ , the two squeegees intersect at a point $P'$ . As $h\rightarrow 0$ , $P'\rightarrow P$ , and $P$ depends on $\theta$ . All these limit intersection points are, of course, points in the edge of the area swept by the sqeegee, and vice-versa. This is the main statement on which this solution is based. *For simplicity, I considered a sqeegee of length $1$ , we'll just have to remember to multiply the area by $k^2$ in the end to get the correct answer. 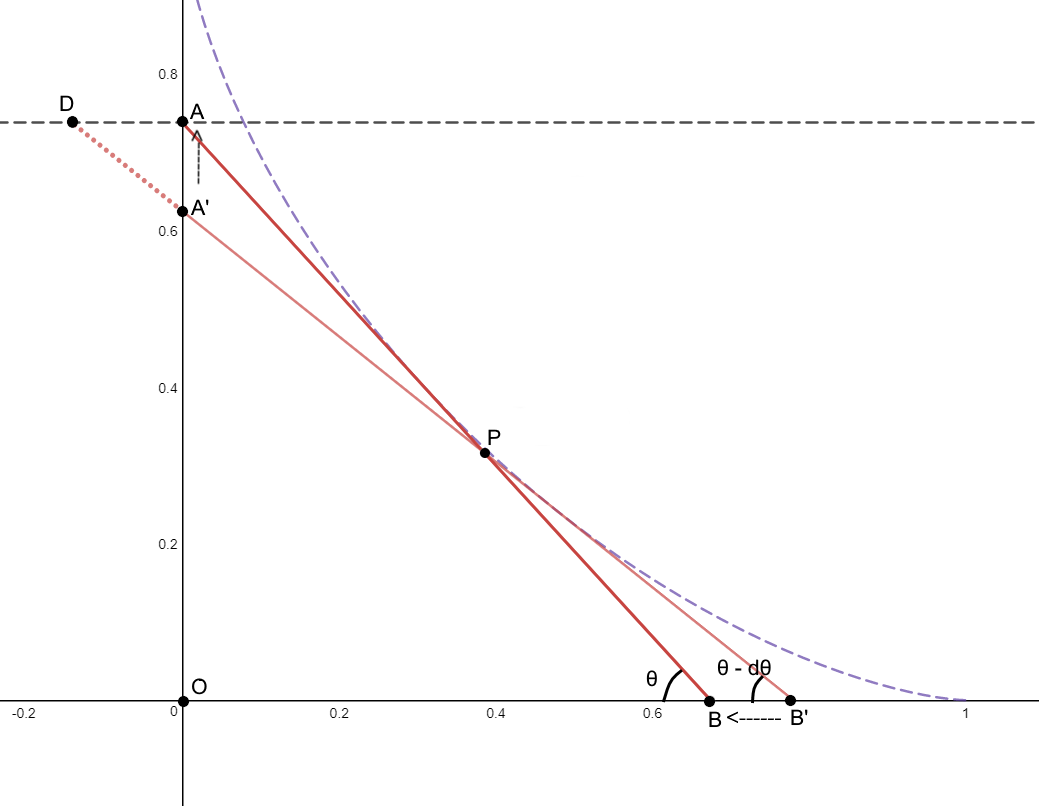Since the squeegee has length $1$ , from triangle $\triangle OAB$ , we see that $\overline { AO }=\sin { \theta }$ , $\overline { BO }=\cos { \theta }$ , and consequently, $\overline { AA' } =\cos { \theta } d\theta$ , and $\overline { BB' } =\sin { \theta } d\theta$ . Now, from triangles $\triangle DAA'$ and $\triangle OA'B'$ , we see that $\angle A\widehat { D } A'=\angle A'\widehat { B' } O$ , so $\overline { DA } =\overline { A'A } \cot { \theta }$ which means $\large \overline { DA } =\frac { \cos ^{ 2 }{ \theta } }{ \sin { \theta } } d\theta$ . Finally, from similar triangles $\triangle DAP$ and $\triangle PBB'$ , $\large \frac { \overline { DA } }{ \overline { AP } } =\frac { \overline { BB' } }{ \overline { PB' } }$ , but we know that $\overline { AP } +\overline { PB } =1$ . Then, making $\overline { PB } =p$ and substituting what we found earlier, we have $\frac{\cos^2\theta}{\left(p-1\right)\sin\theta}=\frac{\sin\theta}{p}$ $p=\left(1-p\right)\tan^2\theta$ $p=\frac{\tan^2\theta}{\left(1+\tan^2\theta\right)}$ $p=\sin^2\theta$ Then, the coordinates of the point $P$ with respect to $\theta$ are $x\left(\theta\right)=\cos\theta-\left(\cos\theta\right)\sin^2\theta$ $y\left(\theta\right)=\left(\sin\theta\right)\sin^2\theta$ Simplifying, we have $x\left(\theta\right)=\cos^3\theta$ $y\left(\theta\right)=\sin^3\theta$ Finally, we know that the area under a parametric curve is $\large \int_{t_1}^{t_2}y\left(t\right)x'\left(t\right)dt$ , so substituting for wat we have, and multiplying by $k^2$ : $\large Area=\frac{2016}{\pi}\int_0^{\frac{\pi}{2}}3\sin^4\left(t\right)\cos^2\left(t\right)dt=189$

Let the square be represented in Cartesian coordinates, with $(0,0)$ as the bottom left corner and $(0,k)$ as the top left corner.

At any time, let $\phi$ be the angle between the squeegee and the vertical. Initially $\phi=0$ and at the end $\phi=\dfrac{\pi}{2}$ .

The squeegee forms a line with gradient $-\cot{\phi}$ and y-intercept $k\cos{\phi}$ . Thus it has the equation $y=k\cos{\phi}-\cot{\phi}x$

A point is considered cleaned if it has been on a squeegee before. In other words, an angle $\phi$ must exist such that $0 \leq \phi \leq \dfrac{\pi}{2}$ which satisfies [y=k\cos{\phi}-\cot{\phi} x]

If we fix $x$ then there will be a range of $y$ values. The curve is given by the maximum y-values. Differentiating $y$ with respect to $phi$ , $\dfrac{dy}{d\phi}=-k\sin{\phi}+\csc^2 {\phi}x$

The $\phi$ yielding the $y_{max}$ is given by $\sin{\phi}=\sqrt[3]{\dfrac{x}{k}}$ $\Rightarrow y_{max}=k\left(1-\left(\dfrac{x}{k}\right)^{\frac23}\right)^{\frac32}$

Integrating, the cleaned area is

$k\int^k_0 \left(1-\left(\dfrac{x}{k}\right)^{\frac23}\right)^{\frac32}dx$

Let $r=\dfrac{x}{k} \Rightarrow dx=k dr$ $=k^2\int^1_0 \left(1-r^{\frac23}\right)^{\frac32}dr$

Let $r=\sin^3 {\theta} \Rightarrow 3\sin^2 {\theta}\cos{\theta}$ $=\dfrac{3k^2}{2}\int^\frac{\pi}{2}_0 2\sin^2{\theta}\cos^4{\theta}d\theta$ $=\dfrac{3k^2}{2}\dfrac{\Gamma(\frac52)+\Gamma(\frac32)}{\Gamma(\frac52+\frac32)}$ $=\dfrac32\left(\dfrac{2016}{\pi}\right)\dfrac{\left(\dfrac32\right)\left(\dfrac12\right)^2(\sqrt{\pi})^2}{6}$ $=\boxed{189}$

Each line ha the form

$F(t,x,y)=-k \sin (t)+x \tan (t)+y=0$

for $0<=t<=\pi/2$ .

Equation of the envelope is all (x,y) such that

$F(t,x,y) = 0, F^{(1,0,0)}(t,x,y) = 0$

Solving for x,y we get

$\left\{x=k \cos ^3(t),y=k \sin (t)-k \sin (t) \cos ^2(t)\right\}$

So we want

$\int_{\frac{\pi }{2}}^0 y(x(t)) x'(t) \, dt = \frac{3 \pi k^2}{32}$

which gives 189 with k above.

I use formula for astroid area. http://www.wolframalpha.com/input/?i=astroid