Stabilize All!
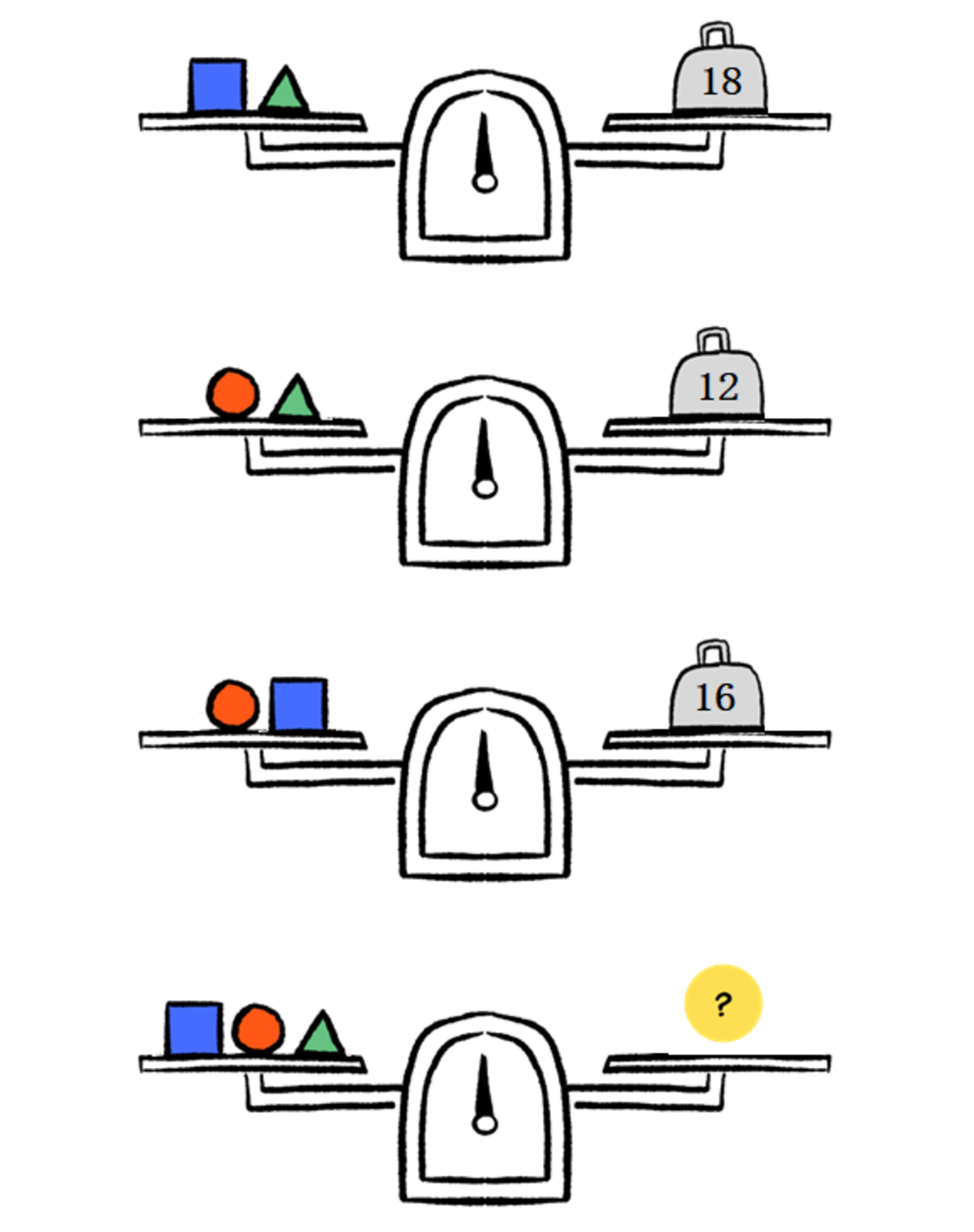
Given the balance scales below, which weight would balance with last scale?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Add them up. 2 squares, 2 circles and 2 triangles equal 46, so one of each is half that.
my approach was a lot simpler s+t=18 s+2c+t=28(i got s+2c+t from adding (s+c)+(t+c)16+12=28 28-18=10 10/2=5
My approach was a little different. As long as you could find one of these values, you should be able to figure out whar s + c + t is, mainly because all three equations are more or less the sum of any of the other two, so you may as well reduce it to the sum of two values.
s + c + t is either equal to:
*c + 18
*s + 12
*t + 16
Now, if you want to look for s, you will get s=11.
(c + s) - (c + t) = 16 - 12
s - t = 4
(s-t) + (s + t) = 4 + 18
2s = 22
s = 11
So now you can find s + c + t as follows:
s + (c + t) = 11 + 12 = 23
Add all the top three scales, by adding LHS and RHS on each scales.
We get 2 ( S + T + C ) = 4 6 , thus its half will be 2 3
11+7+5=23 that is how I got the answer. After plugging in those numbers to the shapes.
Just cancel the 2 t's in two equations and therefore s > c and s - c = 6. With that in mind 11 + 5 = 16 for the next equation and there was a difference of 6 for the 11 and 5. So that's how I solved it.
Let's take the weight of the Square, Triangle and Circle as s, t and c respectively.
According to the question, we can make 3 formulae:
(1) s + t = 1 8
(2) c + t = 1 2
(3) s + c = 1 6
Now we need to convert these formulae into equations in two variables for easier calculation. Starting with Eq. (1), we get
(4) s = 1 8 − t
Then if we substitute the value of s in Eq.(3), we now get:
1 8 − t + c = 1 6
− ( t − c ) = − 2
(5) t − c = 2
Thus now, we have two main formulae to find out the answer. Now all we need to do is substitute the value of t in Eq.(2) or Eq.(5). I have done this in Eq.(5) for simplicity.
t − c = 2
(6) t = 2 + c
Now with substituting the value of t as 2 + c in Eq.(2), we finally get:
2 + c + c = 1 2
2 c = 1 0
c = 5
Now using the value of c as 5 in Eq. (6) and Eq.(3), we get:
s = 1 1 AND t = 7
To find the missing value, we just substitute the value of s , c and t .
Therefore, we find the final answer as follows:
s + c + t = 1 1 + 5 + 7 = 2 3
I have also posted a question on Brilliant. Click here
Visual approach
Algebraic Approach
Let one square be S , one triangle be T and one circle be C .
S + T C + T S + C ⟹ 2 S + 2 C + 2 T ⟹ S + C + T = 1 8 = 1 2 = 1 6 = 4 6 = 2 3