Stack Books at the Edge of a Table
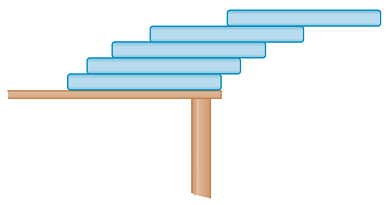 Suppose you have a large supply of books, all the same size, and you stack them at the edge of a table, with each book extending farther beyond the edge of the table than the one beneath it. Is it possible to do this so that the top book can extend any distance at all beyond the edge of the table if the stack is high enough? Try it yourself with a deck of cards.
Suppose you have a large supply of books, all the same size, and you stack them at the edge of a table, with each book extending farther beyond the edge of the table than the one beneath it. Is it possible to do this so that the top book can extend any distance at all beyond the edge of the table if the stack is high enough? Try it yourself with a deck of cards.
Hints: Consider centers of mass.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Use the following method of stacking: The top book extends half its length beyond the second book. The second book extends a quarter of its length beyond the third. The third extends one-sixth of its length beyond the fourth, and so on.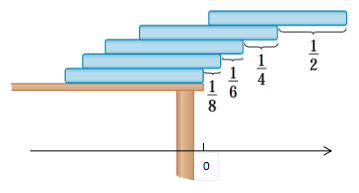 Let
m
and
L
be the mass and length of each book, respectively. And take the edge of the table as the origin of number line as shown.
When we have
n
books, denote the center of mass of
n
books by
c
n
, and the distance that the top book extends beyond the edge of the table
d
n
.
When there are
(
n
+
1
)
books, by the method of stacking, we get
c
n
+
1
=
(
n
+
1
)
m
n
m
(
c
n
+
2
n
L
)
+
m
(
−
2
L
)
=
n
+
1
n
c
n
=
n
+
1
n
n
n
−
1
…
2
1
c
1
=
−
2
(
n
+
1
)
L
<
0
.
Therefore, these books couldn't collapse. In this case, we have
d
n
+
1
=
2
L
(
1
+
2
1
+
3
1
+
…
+
n
1
)
.
Since harmonic series
∑
k
=
1
∞
k
1
is divergent, the top book can extend any distance at all beyond the edge of the table as long as the stack is high enough, that is, the answer is
Yes
.
Let
m
and
L
be the mass and length of each book, respectively. And take the edge of the table as the origin of number line as shown.
When we have
n
books, denote the center of mass of
n
books by
c
n
, and the distance that the top book extends beyond the edge of the table
d
n
.
When there are
(
n
+
1
)
books, by the method of stacking, we get
c
n
+
1
=
(
n
+
1
)
m
n
m
(
c
n
+
2
n
L
)
+
m
(
−
2
L
)
=
n
+
1
n
c
n
=
n
+
1
n
n
n
−
1
…
2
1
c
1
=
−
2
(
n
+
1
)
L
<
0
.
Therefore, these books couldn't collapse. In this case, we have
d
n
+
1
=
2
L
(
1
+
2
1
+
3
1
+
…
+
n
1
)
.
Since harmonic series
∑
k
=
1
∞
k
1
is divergent, the top book can extend any distance at all beyond the edge of the table as long as the stack is high enough, that is, the answer is
Yes
.