Stacked Carts
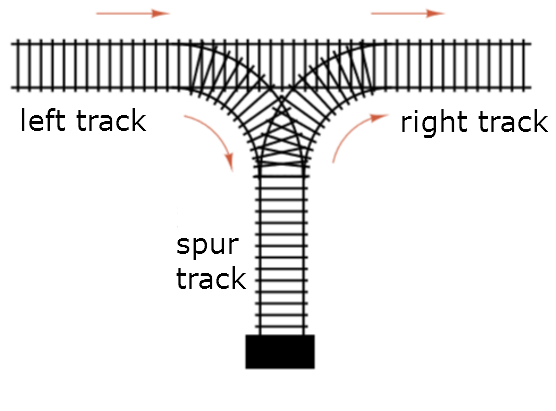
There are carts arranged from 1 to on the left track. There are two commands available to the operator:
-
push: move the rightmost cart from the left track to the top of the spur track -
pop: move the topmost cart from the spur track to the right track.
Using these commands, in how many ways can we permute the carts as they are being queued up in the right track? Assume there are 16 carts.
For example, let us say there are 3 carts. Consider the sequence of commands
push, pop, push, push, pop, pop
-
pushpushes cart 3 to the spur track. -
poppops cart 3 to the right track. -
pushpushes cart 2 and cart 1 to the spur track. -
poppops cart 1 and cart 2 to the right track.
The new sequence of carts on the right track is
[2, 1, 3]
.
It turns out, that there are 5 ways the new sequence of carts can be in, when
The answer is 35357670.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let us try a recursive solution first:
But that is probably an inefficient solution. Let's try something else.
Consider any valid sequence of
pushandpop. The following must be true:pushes aspops. Otherwise, we'd get a stackoverflow or keep a cart in the spur forever.poped before it waspushed.And now consider the well known properties of bracketed sequences like
(())()(). They have the same rules:(as).)that precedes its corresponding(.So, if we replaced
pops andpushes with(and), we'd get a bracketed sequence.As we are aware of, the number of such sequences are the Catalan Numbers