Stacked Spheres

Note that the centers of the spheres will form a regular tetrahedron of side length 20. Using the pythagorean theorem twice, we find that the height of that tetrahedron is $10 \sqrt{6}/3$ . The base of the tetrahedron is 10 units above the ground, so the distance from the ground to the center of the fourth sphere is $10\sqrt{6}/3 + 10$ . We then have: $h + 10 = 10\sqrt{6}/3 + 10$ so $h = 10\sqrt{6}/3$ , thus $h^2 = 800/3$ Which yields $a+b=803$ .

[Latex edits - Calvin]

You can think of the radius of the 4 spheres forming an equilateral pyramid whose sides have a length of 20 (twice the radius). Compute for the height of that pyramid and you'll get h = sqrt(800/3). That height, h also happens to be the distance h searched for in the problem. since h^2=800/3 and 800 and 3 happen to be coprime, then a+b = 803.

The centers of the four spheres are vertices of a regular tetrahedron with edges of length 20. If the height of the tetrahedron is $h$ , then the distance from the table to the top of the fourth sphere is $10 + h - 10.$ Hence, the distance from the table to the bottom of the fourth sphere is $h$ .

The height $h$ can be calculated using the Pythagorean Theorem. From the top vertex, drop a perpendicular to the base, which intersects at the center of the equilateral base. The height of the equilateral triangle is $\frac {20 \sqrt{3} }{2}$ , and the center is located one-third of the way from the base. Hence, we have $20^ 2 = h^2 + \left(\frac { 20 \sqrt{3} }{3} \right)^2$ , which gives $h^2 = \frac {800}{3}$ . Hence $a + b = 800 + 3 = 803$ .

For those whose 3-D knowledge is limited to spheres only.
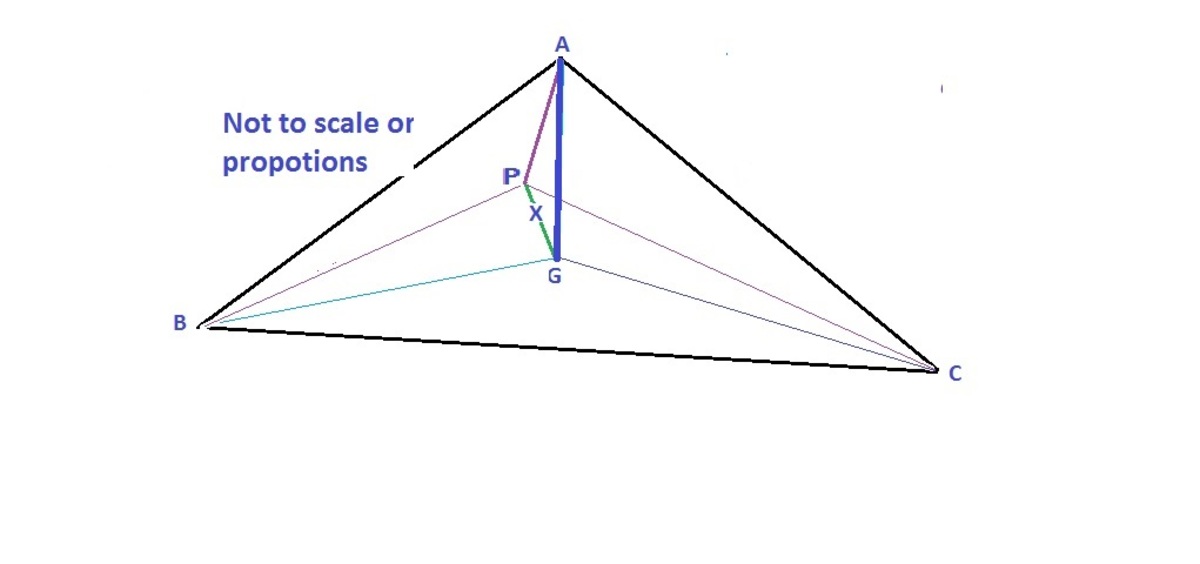
Let A, B, C be the centers of the bottom spheres, P of the top sphere.
Easy to see that ABC is equilateral triangle with sides 20 and 10 above the ground.
G the centroid of ABC, will be vertically below P because of symmetry at a distance of say x below P. That is, x=GP and perpendicular to ABC.
From A ( it could be B or C also ), $AG= \dfrac{2}{3} * \dfrac{\sqrt3}{2} * 20 = \dfrac{20}{\sqrt3}~ for ~the~ equilatral ~triangle.$
$AP=20.~ Thus~ we~ have~ a~~ right ~angled~ triangle ~~AGP.$
$x^2 =GP^2=AP^2-AG^2=20^2-(\dfrac{20}{\sqrt3})^2 = \dfrac{800}{3}\\ \implies~x=\sqrt{ \dfrac{800}{3} }. \\ \therefore~botom~ of~ the ~top ~sphere~ is~~ x-10 ~from ~ G.\\ But ~G ~is~10~above~the~ground.\\So, ~botom~ of~ the ~top ~sphere~is~x-10+10=x= \sqrt{ \dfrac{800}{3} }=h. \\h^2=\dfrac{800}{3} =\dfrac{a}{b}.~~a+b =\boxed {803}$ .