Stacked squares in a triangle

Geometry Level 3

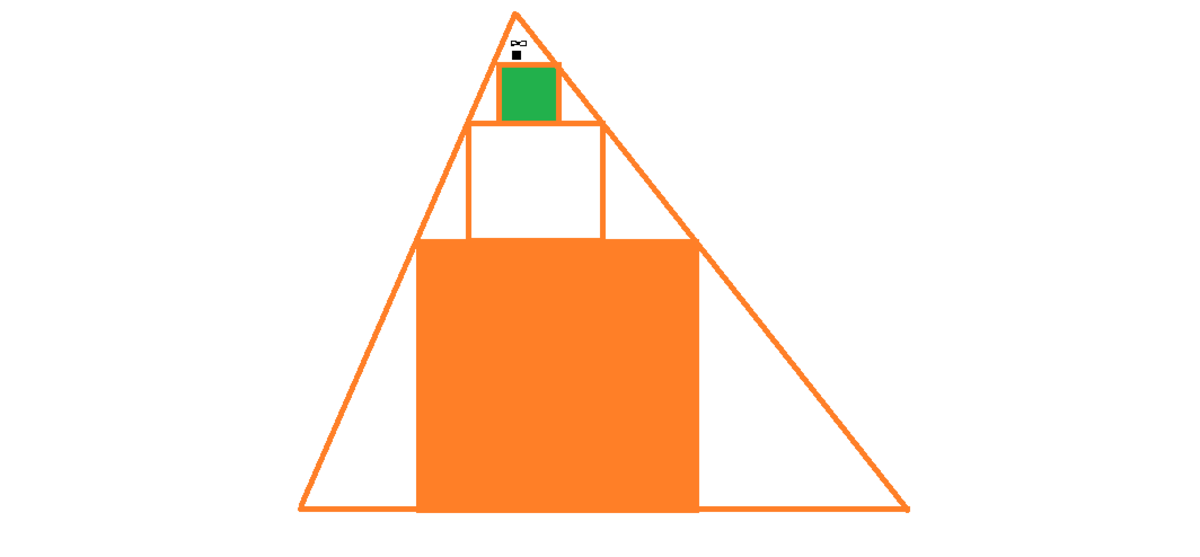Given a triangle with a base of 9 inches and height of 8 inches,

Suppose we stack squares infinitely in the triangle as shown in the figure above, what is the total area of all the squares in the triangle in square inches ?


The answer is 23.04.

View wiki
Vijay Simha by Vijay Simha , 47, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Rab Gani
Jun 3, 2020

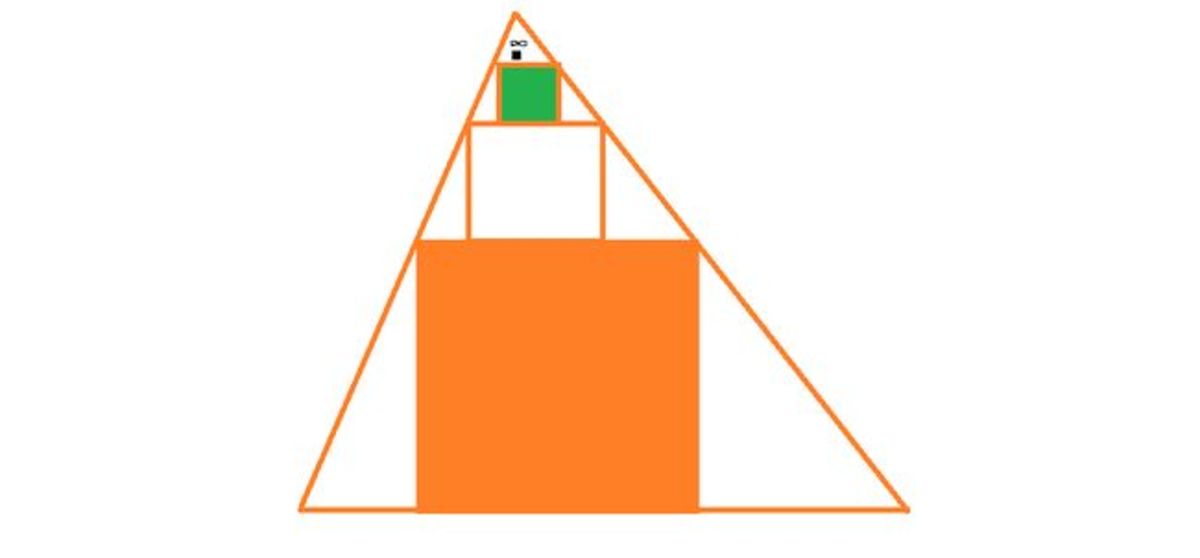
Using similarity , and let the sides of squares of decreasing values are a, b, etc. So we find the total height of similar trapezium a/(1-b/a) = 8. And from similarity we have b/a = a/9. From these 2 equations, we find a=72/17. The total area of squares = a^2 /[1 - (b/a)^2] = 23.04

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Vijay Simha
May 27, 2015

Clearly the length of the side of the base (orange) square is (b h/(b+h)), and its area is A1 = (b h/(b+h))^2

The length of the side of the white square is (b h^2/(b+h)^2) and its area is A2 = (b h^2/(b+h)^2)^2

Similarly A3 is (b*h^3/(b+h)^3)^2

A1, A2, A3 .... infinity form a geometric sequence the sum of whose terms is given by a/(1-r) where a = A1 and r is the common ratio which is equal to h^2/(b+h)^2

Total area is therefore bh^2/(b + 2h).

Substituting the values of b = 9 and h = 8,

We get the total Area to be = 9*64/(9+16) = 576/25 = 23.04

0 Helpful 0 Interesting 0 Brilliant 1 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...