Stacking cylinders
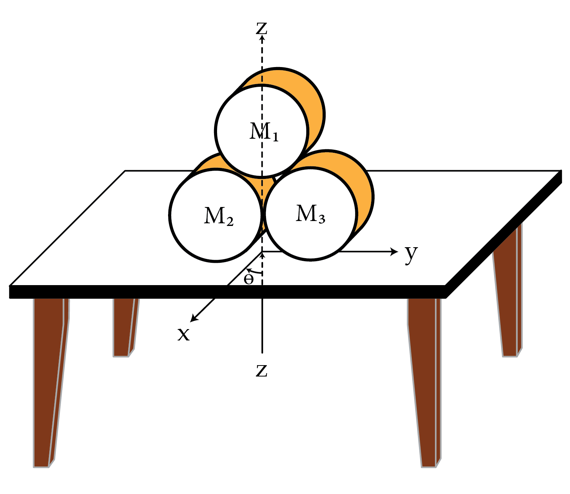
Three cylinders, all of the same mass, are stacked on a table as shown in the figure. There is enough friction between the cylinders and the table such that the cylinders remain at rest.
Let and , respectively, be the horizontal and the normal forces of the table on one of the cylinders. When is a minimum, what is the ratio ?
Note:
The z-axis is vertical, x and y-axis are along the table. The angle shown in the diagram is .
The answer is 0.0893.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let W be the weight of one of the cylinders. The total weight is then 3W, and so the normal force of the table F n on a cylinder is 3W/2. Now let us consider the right hand cylinder. There are three points of contact on this cylinder, where the top cylinder touches, where the left cylinder touches, and where the table touches. The top most cylinder touches at an angle of 60 degrees with respect to the horizontal and exerts a force F t , r towards the center of the right hand cylinder and a force F t , h tangent to the right hand cylinder. The table similarly exerts a force F p , r towards the center and F p , h tangent to the cylinder. The left hand cylinder only exerts a force F L , r towards the center of the right hand cylinder by symmetry.
We first note that to balance torque on the right-hand cylinder F t , h = F p , h = F h . We can then apply a force balance in the x,y directions:
W + F h s i n 3 0 + F t , r s i n 6 0 = 3 W / 2 , F L , r + F t , r s i n 3 0 = F h + F h c o s 3 0 .
If F h is a minimum, that means F L , r is zero (no extra force needed), so we can solve for F h = W / ( 4 + 2 3 ) and hence F h / F n .