Stacking It Right
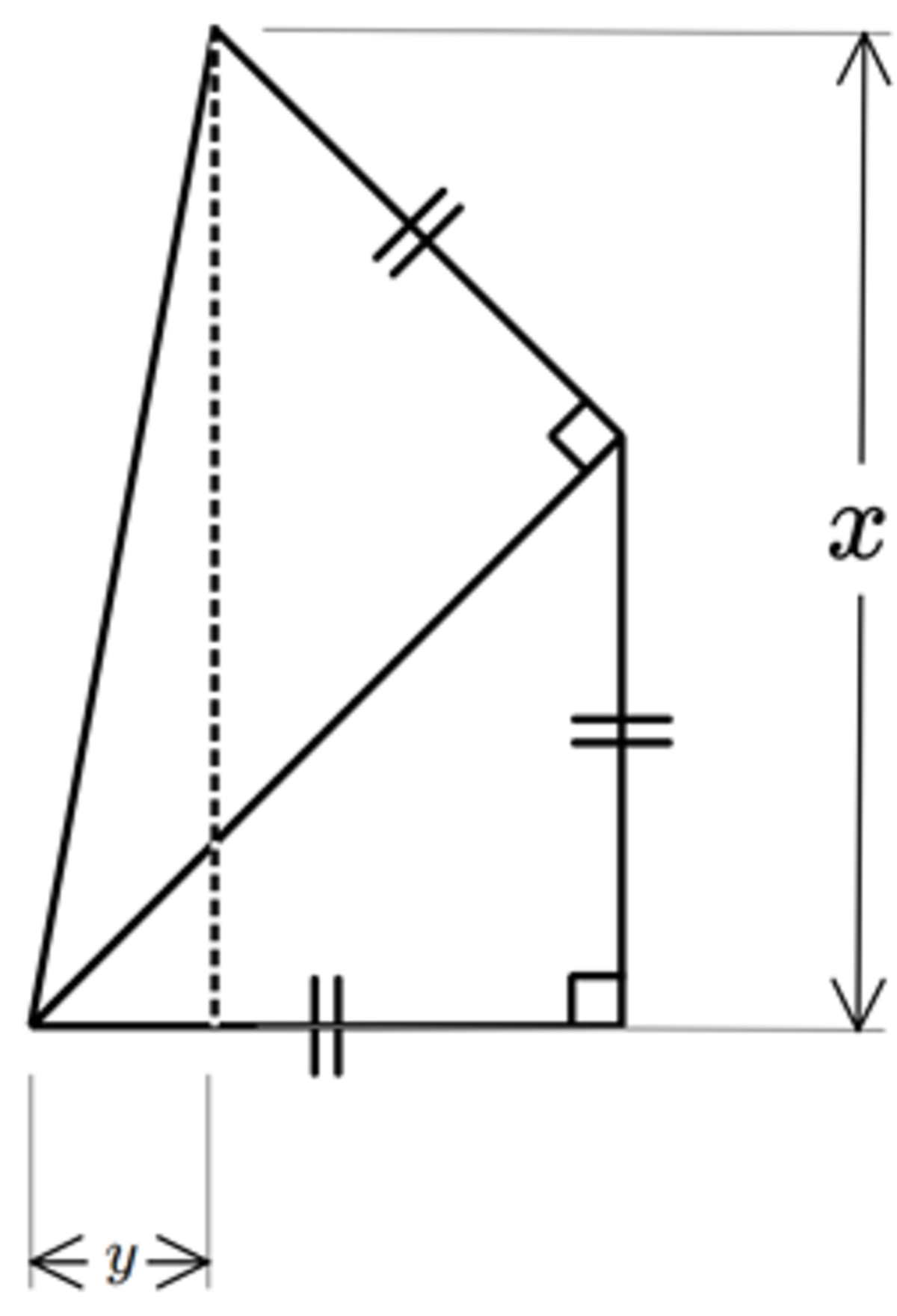
The above shows two right triangles stacked on one another. What is the value of the ratio y x ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Relevant wiki: Tangent - Sum and Difference Formulas
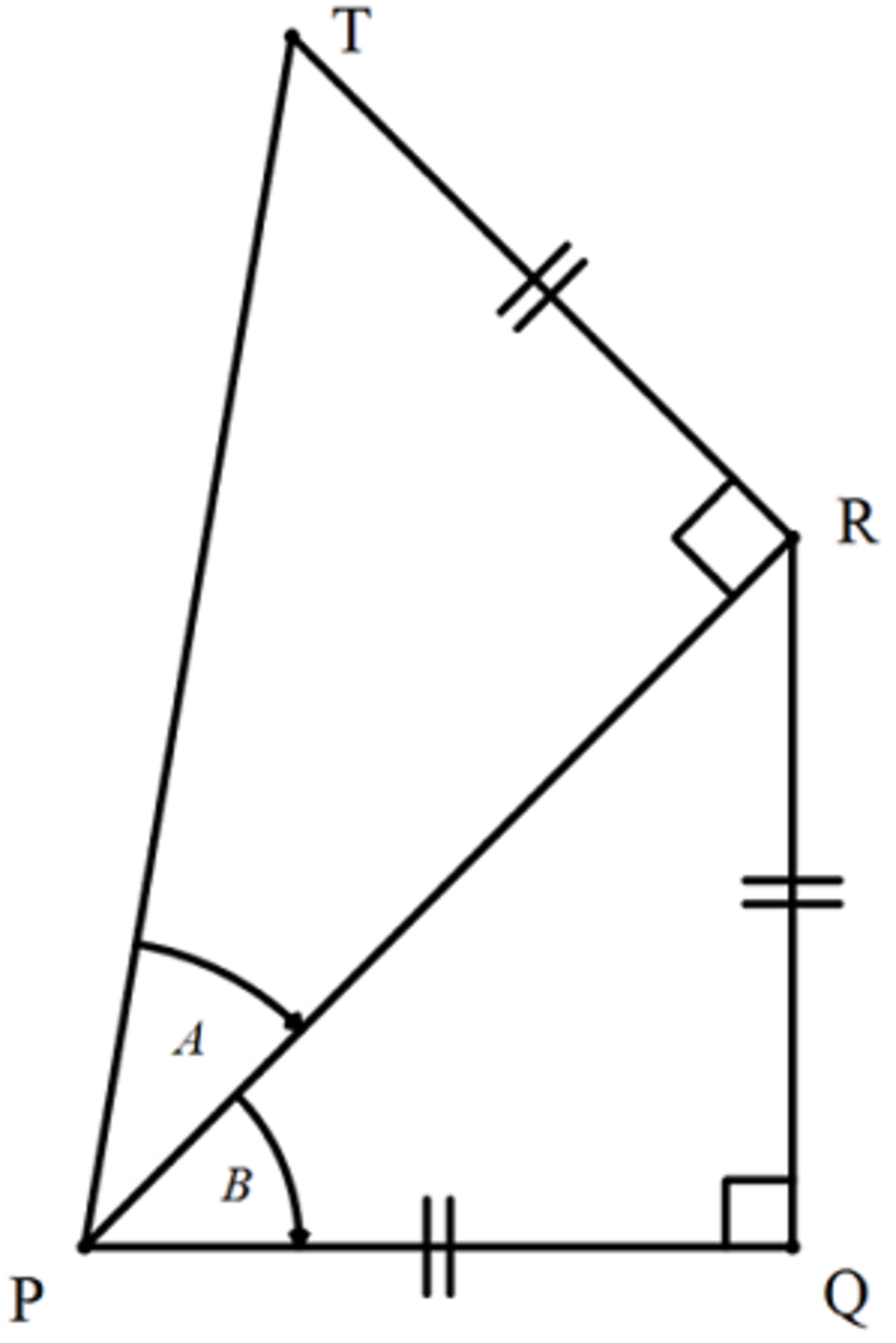
The ratio y x can expressed as tan ( A + B ) .
Let P Q = Q R = R T = k . Then by Pythagorean theorem , P R 2 = P Q 2 + Q R 2 = k 2 + k 2 ⇒ P R = k 2 .
So tan B = P Q Q R = k k = 1 and tan A = P R R T = k 2 k = 2 1 .
Hence, by compound angle formula ,
y x = tan ( A + B ) = = = = = = 1 − tan A tan B tan A + tan B 1 − 1 ⋅ 2 1 1 + 2 1 2 − 1 2 + 1 ( 2 − 1 ) ( 2 + 1 ) ( 2 + 1 ) 2 2 − 1 2 + 1 + 2 2 3 + 2 2 = 8 + 9 .
Let the leg of the right isosceles triangle have length A . Then { x = A + A sin 4 5 ° y = A − A sin 4 5 ° We can then find the ratio by factoring out A from the numerator and denominator: y x = 1 − 2 2 1 + 2 2 = ( 2 − 2 ) ( 2 + 2 ) ( 2 + 2 ) 2 = 3 + 2 2 = 8 + 9