Stacking Squares in a Triangle!

Consider one trapezoid layer, where the short leg of one of the side triangles is $x$ , which makes the side of the square $\sqrt{3}x$ .

Then the ratio of the area of the square to the area of the trapezoid is $\frac{(\sqrt{3}x)^2}{(\sqrt{3}x)^2 + \sqrt{3}x^2} = \frac{1}{2}(3 - \sqrt{3})$ .

Since this ratio is maintained for the infinite layers of trapezoids in the diagram, and since the area of the whole equilateral triangle is $\frac{\sqrt{3}}{4} \cdot 1^2 = \frac{\sqrt{3}}{4}$ , the sum of the areas of the stacked squares is $\frac{1}{2}(3 - \sqrt{3}) \cdot \frac{\sqrt{3}}{4} = \boxed{\frac{1}{8}(3\sqrt{3} - 3)}$ .

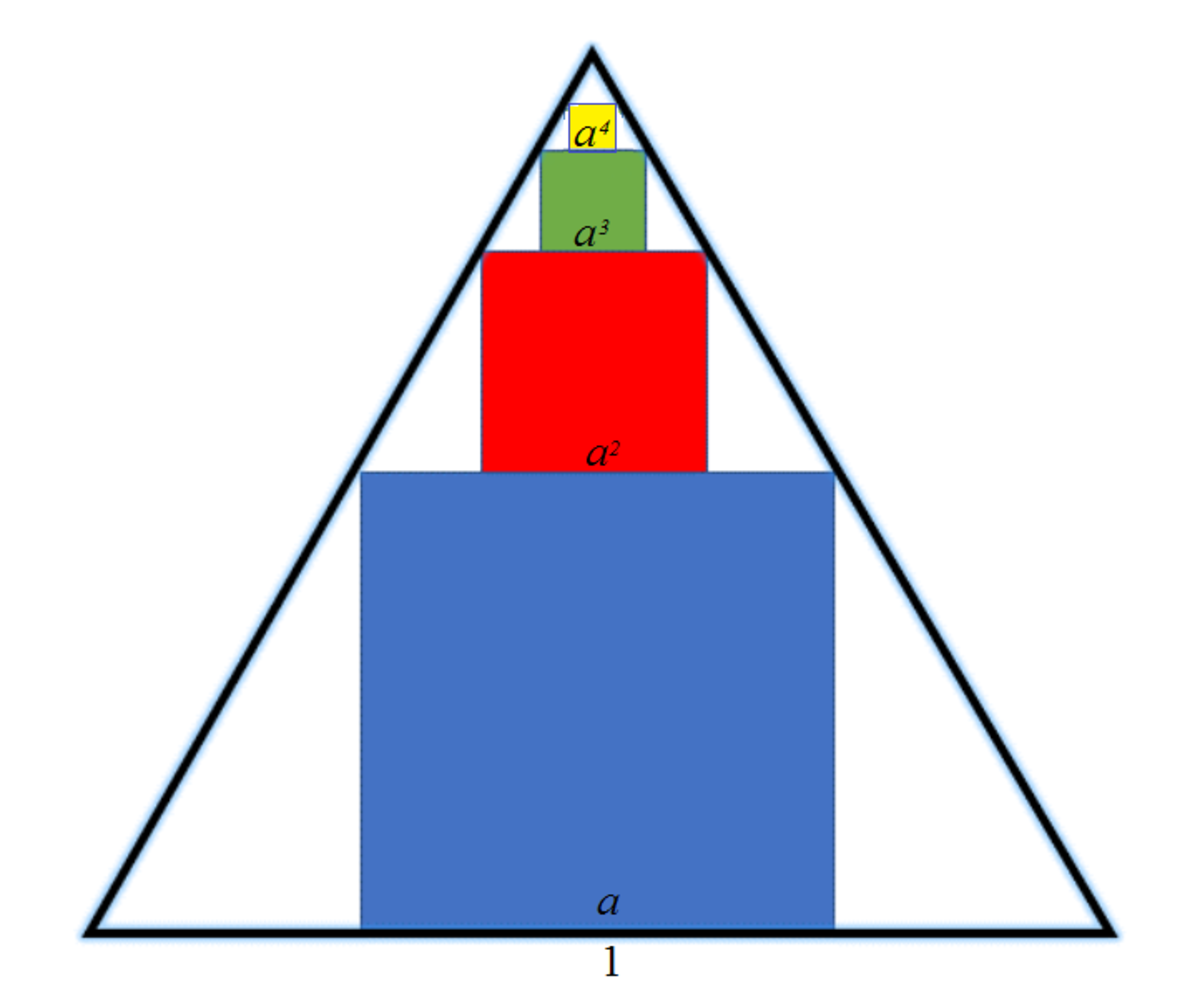
Order the square from the large to small. Let the first square to have a side length of $a$ . Then the ratio of side length of first square and the base of the triangle is $\dfrac a1$ . Because the pattern repeats, the ratio of the side length of the second side length and the base of second triangle is also $\dfrac a1 = \dfrac {a^2}a$ . Therefore the side length of the second square is $a^2$ . That of the third is $a^3$ and so on. The the sum of areas of all the square is given by:

$\begin{aligned} S_A & = a^2 + a^4 + a^6 + \cdots = \frac {a^2}{1-a^2} & \small \blue{\text{From }2 a \tan 30^\circ + a = 1 \text{, we have}} \\ & = \frac {3(7-4\sqrt 3)}{4(3\sqrt 3-5)} = \boxed{\frac {3(\sqrt 3-1)}8} & \small \blue{a = \sqrt 3(2-\sqrt 3), a^2 = 3(7-4\sqrt 3)} \end{aligned}$

Yes of course. Here it is :

Area of the largest square is

$(\frac{\sqrt 3}{\sqrt 3+2})^2$ ,

the next smaller one is

$(\frac{\sqrt 3}{\sqrt 3+2})^4$ ,

and so on.

Hence the total area of all the squares is

$(\frac{\sqrt 3}{\sqrt 3+2})^2\times \dfrac{1}{1-(\frac{\sqrt 3}{\sqrt 3+2})^2}=$

$\dfrac{3}{4(\sqrt 3+1)}=\boxed {\dfrac{1}{8}(3\sqrt 3-3)}$ .

Thank you everyone for sharing your solutions.