Stacks of Equal Height
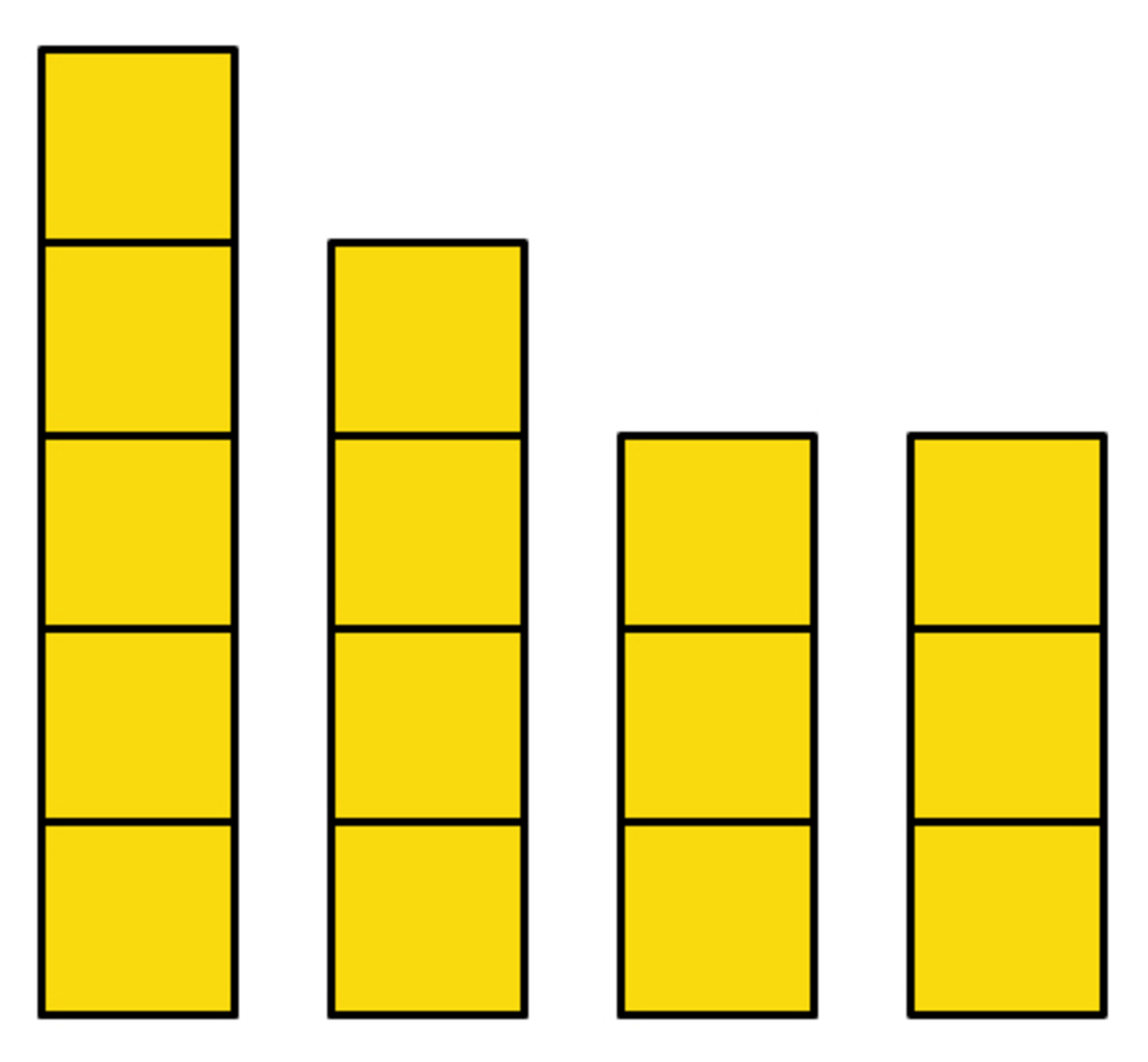
I have 4 stacks of blocks as shown in this image.
Each move, I choose a stack, take as many blocks as I want, and move them all to another stack.
What is the minimum number of moves I have to make in order for the remaining stacks to have the same height?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We can do it in 2 moves.
We have 5 + 4 + 3 + 3 = 15 blocks altogether. We can make 3 stacks of 5 blocks (please note, that it is not required to keep all 4 stacks) in 2 moves:
First move: Take all 3 blocks of the 4th stack, and put them on the 3rd stack. As a result we have now 5, 4 and 6 blocks in the 1st, 2nd and 3rd stack, respectively.
Second move: Take 1 block from the 3rd stack, and put it on the 2nd stack. As a result we have now 5 blocks in each of the 3 stacks.
It is also easy to see, that it cannot be done in less steps (in this case, it would mean just in 1 step: in each step. we can only change the number of cubes in just 2 stacks. If we choose any 2 of the 4 stacks given, it is impossible to match the number of blocks in both of the other two stacks (which then have to be the same height (in this case, it would mean the 3rd and 4th stacks with 3 blocks each) and we cannot make the 1st and 2nd stacks with 5 and 4 blocks to match them in one step).
If forming a new stack is allowed as well, we have another (3rd, as we can interchange the 3rd and the 4th stacks in the wording of the solution above to get the 2nd solution) two step solution:
First move: Take 3 blocks from the 1st stack, and form a new, 5th stack out of them. As a result we have now 2, 4, 3, 3 and 3 blocks in the 1st, 2nd, 3rd, 4th and 5th stacks, respectively.
Second move: Take 1 block from the 2nd stack, and put it on the 1st stack. As a result we have now 3 blocks in each of the 5 stacks.