Staircase Of Hats
Frustrated at Alice and Bob's success at guessing his number (see here ), Jack decides to vent his anger by imposing another 'impossible' challenge to Helen, Jon, George, and Ava.
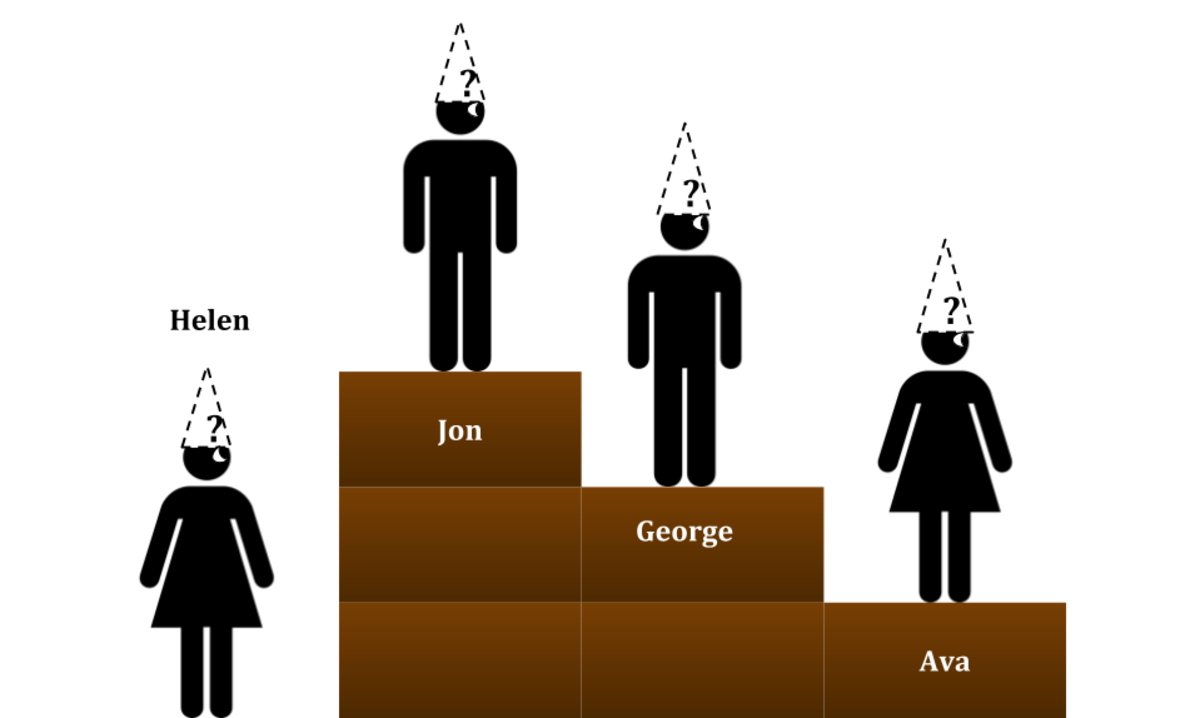
Jack says, "You will be standing on stairs, facing forward (to the right, as shown below). Then, I will give all four of you hats drawn randomly from a set of three black hats and one white hat. Now, each of you cannot look back. So,
Helen can only see Jon;
Jon can only see George and Ava;
George can only see Ava;
Ava can see no one.
You are not allowed to tell anyone the color of your hat; you are only allowed to say that you know, or don't know, the color of your hat. The game ends when everyone knows the color of their hat, or you all give up."
Then their conversation goes as follows:
Jon:
"I do not know the color of my hat."
Ava, George, Helen:
"Then I also know the color of my hat."
Jon:
"Then I also know."
Who was wearing the white hat ?
Assume that whenever someone knows the color of their hat, they state it immediately.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Jon's first statement gives valuable information to both George and Ava: in fact, the only way for Jon to not know the colour of his hat is if both George and Ava are both wearing black hats.
After George and Ava make their declaration, Helen, through the steps we have followed, now knows the colour of her hat, as she knows the colour of Jon's hat and has deduced the colour of George and Ava's hats.
Jon's situation may seem hopeless, forced to choose between black and white. However, remember that if a person knows their hat colour, they must say it immediately. If Jon had been wearing white, Helen would have known immediately that her hat was black, as there is only one white hat. Thus, Jon's hat must be black, and Helen's white.
The solution is, thus:
Helen - White
Jon - Black
George - Black
Ava - Black