Standing on a Swing
A swing is in motion with a girl sitting on it. If the girl stands up on the swing when the swing is at the lowest point, what happens to the time period of the swing?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
What about the amplitude of the oscillations? Will it decrease or increase?
This particular problem assumes the angular moment of inertia can be ignored. When the girl stands up her moment of inertia is greater than when she is sitting and while that will reduce period of the pendulum, the rising center of mass is the overriding factor until the center of gravity approaches the pivot point. For a physical pendulum that is not a point mass: Period T = 2 * pi * sqrt( Inertia _ about _ pivot / (mass * g * Len _ to _ centermass)) The trick is to realize that Inertia_ about _pivot is a function of shape, but also Len _to _centermass).
Log in to reply
This is not a physical pendulum where a rigid body is hinged at one of its point. Rather, it is more of a simple pendulum only.
Please explain how extending the legs down (i.e., away from the fulcrum [assuming the body remains fixed]) raises the body's center of mass toward the fulcrum. That's the key and it's not intuitive to me.
Log in to reply
We are not extending the legs while remaining in the sitting position, we are standing up in the swing, thus the center of mass rises and the time period decreases.
The claim the the period will be lessened neglects one important factor - air resistance. the girl standing will present a greater surface area to the air, thereby increasing air resistance and slowing the swing, thereby increasing the time to complete one oscillation.
Darn - this got me! I knew the formula inside out but rushed my thinking. Since mass is not part of the equation, but length of the pendulum is indeed part of the equation I see now that when she sits down the whole pendulum length extends to her feet BELOW the swing hence a longer period than when she is stood up.
Without remembering T = 2 π g l : Imagine girl stands up immediatelly at lowest point (where speed is maximal and acceleration is zero). This does not change acceleration and speed. However, the center of mass moves up, this shortens the effective length of the swing (the radius of trajectory) and therefore shortens path (trajectory is now part of a smaller circle). A shorter distance will be travelled in a shorter time given the same speed and acceleration.
Why did you choose the lowest point? Will the answer change if the girl stands up at the extreme point?
Log in to reply
I took the reference point because of the formulation of the problem. At an extreme, it is more interesting. The speed is zero and the component of gravity along trajectory is maximal, so acceleration is maximal as well. Let's say you have an angle Φ between the radius of trajectory drawn through lowest point and the radius drawn through an extreme point. Now, if you stand up vertically at extreme, the center of mass moves up vertically, but not along the radius. This has two effects: i) the change of the effective length (radius), and ii) a slight increase of the angle Φ + Δ Φ , or maximal amplitude (or not so slight increase, depending on the height of the girl relatively to the length of the rope).
If Φ l ≪ l , period can be assumed not depending on amplitude and determined by length (l) alone. In fact, this approximation is required for formla T = 2 π g l to work. In this case, T decreases as the effective length of trajectory is determined by the shortening of l (we effectively took Δ Φ ∼ 0 ).
Let's consider another extreme case, Φ l ≫ l . In this case, a change of l is less important than a change of Φ . Let's take Φ = π / 2 . In this case Δ Φ = a t a n ( h / l ) where h is vertical shift of the center of mass (at extreme). Depending on h/l, Δ Φ can be made comparable to Φ . This can noticeably increase amplitude and thus elongate trajectory whereas keeping the same initial speed and acceleration (starting at extreme). So, with noticeably longer trajectory, one can expect that one swing will take more time (we effectively took l = const, but 1 ≪ Φ Φ + Δ Φ < 2 ).
Log in to reply
Great explanation, thanks a lot!
Thanks for the detailed explanation.
Do the laws of motion and mass differ in real time? Because if you stand up on a swing at the low point you are accelerating the mass upwards, diverting the energy upwards instead of with the motion of the pendulum. If you stand up with sufficient velocity, the swing will stop altogether.
Log in to reply
For standing up are you taking up the energy kinetic energy of the swing or putting in your muscular energy?
Bad maths problem. If the girl stands up when the swing is at the lowest point, she is going to disrupt the move and the swing will slow down. 😒
Log in to reply
How does she standing up decreases the speed of the motion? Even if the speed is decreased the amplitude of oscillation will decrease but the time period does not depend on the amplitude of oscillation.
Nice &Logical problem
If the girl stands up toward the point of rotation, the angular momentum is not changed but the effective length of the pendulum (center to center of mass) is reduced => the swing accelerates by conservation of angular momentum.
T =2pi*√l/g when l decreases T decreases
It seems like resistance at that point would slow the swing!
The swing takes less time to complete one oscillation. First consider the girl sitting on the swing. Clump the mass of the chair and the girl into one point called the center of mass . From here we have a simple pendulum.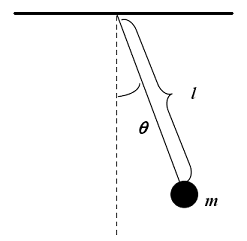
From classical physics, the period of oscillation is T = 2 π g l . With this model and equation, we can solve the problem.
Once the girl is standing up, her center of mass actually rises, causing the length l to decrease, which decreases the period. As a result, the swing takes less time to complete one oscillation.