Star Study - 10 pointed total
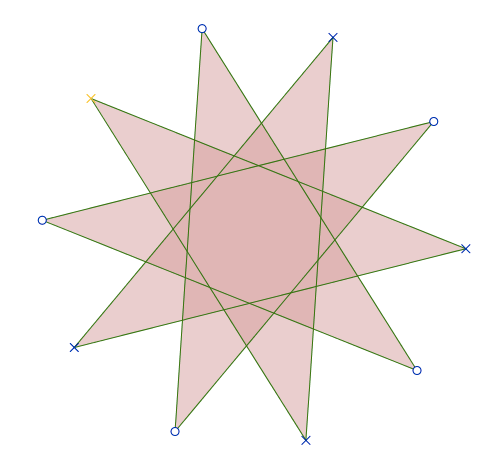 Consider a regular 10 pointed star, where each vertex is connected to the 2 vertices that are almost diagonally opposite. What is the sum of the internal angles (in degrees)?
Consider a regular 10 pointed star, where each vertex is connected to the 2 vertices that are almost diagonally opposite. What is the sum of the internal angles (in degrees)?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
But you haven't explained the crucial statement, which is not obvious, "The angle from one vertex A to the two opposite vertices B and C is one-half the size of the central angle BOC"
Log in to reply
Sorry for the incomplete explanation. There is a theorem in (Euclidean) geometry which gives this half-size relationship between the central angle and the vertex angle when they subtend the same arc on the circle
Thank you. Enjoy applying my mind.
And if you trace the figure in this problem you will see that it comprises two separate 5-point stars. Problem 1 solution shows that the internal angles of each star totals 180 degrees. Therefore the two stars' total internal angles will be 2 x 180 = 360 degree s
Just a sum of triangles.
First, notice that in the middle of the many lines there is a regular pentagon. The interior angles of a pentagon add up to 540 degrees, so each of the 5 angles is 540/5 = 108 degrees. Two of those angles form straight lines (180 degrees) with the two equal angles of the isosceles triangle formed by a vertex of the star and a side of the pentagon. So the two equal angles must be 180-108 = 72 degrees each. That leaves 180-(72+72) = 36 degrees for the angle at the vertex of the 10 pointed star. Since there are 10 points, there is 10*36 = 360 degrees total in the interior angles.
All polygon internal vertices' angles always sum up to 360.
Problem 5 disagrees
Consider a Triangle. Sum of internal angle=180. Consider a square, sum of internal angle=360. Pentagon=540, Hexagon= 720. And so on...
notice it's just 2 stars stacked and we see it from above...
a single star have the inner pentagon, 5 point, each 108 degrees
now you know the single point at star 'hand' have 36 degrees
just multiply it by 10 ....and viola... 360 degrees is the answer
just break this diagram into two 5-pointed star. Now you can easily see that the pentagon formed inside each 5 pointed star, internal angles adds up to 540 degrees. Therefore each angle = 108. Thus the vertex of star constitute angle= 36. Thus the sum total becomes 36*10=360
it is true for all polygonal vertices internal angles..it is always 360
0 x (360/10) = 360 degrees
This is having 10 sided polygon inside whose sum of all anles is 1080,similar to 5 star angles this forms 10 star angles and their sum is 360 degree. K.K.GARG,India
Look at the image carefully and you will see that this star has been made by superimposing 2 5-pointed stars on one another. So, the angle at the vertex will be 3 6 ∘ , as per previous problems in this set. Therefore, sum of internal angles is 3 6 0 ∘
Any segment which tie two point of a circunsference is ¨seen¨ by the points of that circunsference by either a half of the angle seen from the center or its complementary (a diameter is always seen with a 90 degrees angle from both sides), a five points star uses a penthagonal distribution with 72 degrees from the center which means that the star internal angles are 36 degrees.
Draw a circle with center at O and the ten vertices lie on the circle. The angle from one vertex A to the two opposite vertices B and C is one-half the size of the central angle BOC. Five such central angles complete one 360 degrees revolution. So angle BOC = 360/5 and vertex angle BAC = 360/10. So the total of ten such vertex angles equals 10 x (360/10) = 360 degrees