Five-Pointed Star
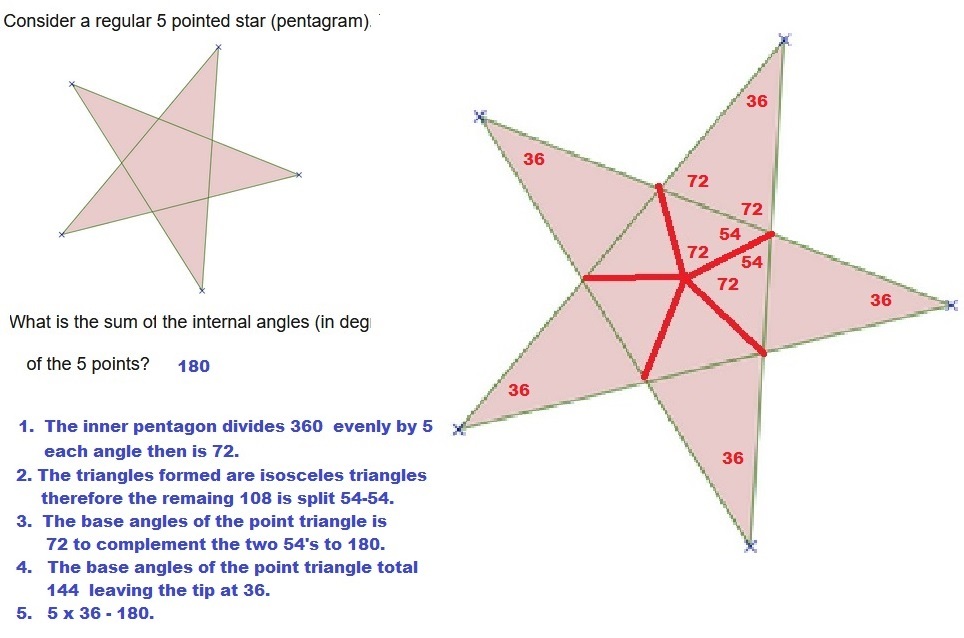
 Consider a regular 5 pointed star (pentagram). What is the sum of the internal angles (in degrees) of the 5 points?
Consider a regular 5 pointed star (pentagram). What is the sum of the internal angles (in degrees) of the 5 points?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
24 solutions
The internal Pentagon has all its angles = 108 each So the outer triangles have its base angles as 72 and 72 So the outer triangles have its top angle as 36 each So the sum will be 36 x 5 = 180
Yes, yes, yes, but the starting point is no knowledge of pentagrams, or rules.
Just using the star, the degrees cannot be deduced from the star itself, without measuring the degrees by hand.
Therefore it is a dumb question.
Log in to reply
It says that the pentagram is regular, which means that the pentagon is also regular, and so has the 108 degree interior angles.
What's the "property of linearity"? May someone please point me to a wiki page about that. Thanks.
boi... forget about triangulating the pentagon. I thought the sum of the angle of the pentagon is 360 -_-
Consider the following picture, obtained by drawing a circle whose points are the points of a star:
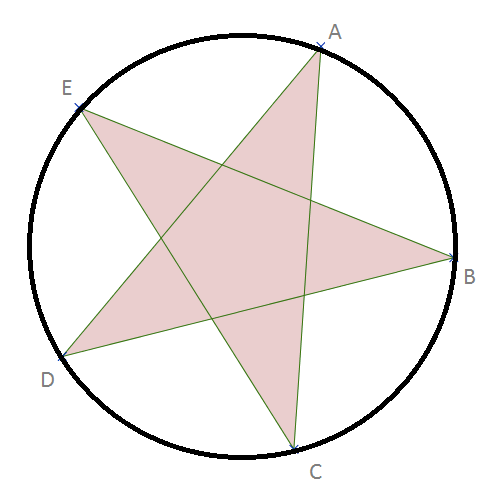
Notice that the arcs: AB=BC=CD=DE=EA, and that AB+BC+CD+DE+EA=360
Remember that the angle of an arc is the double of the inscribed angle.
So CAD=DBE=ECA=ADB=BEC=AB/2=BC/2=CD/2=DE/2=EA/2
Therefore: CAD + DBE + ECA + ADB + BEC = 180
I haven't taken a math class since college, 8 years ago, so I'm trying to refresh. After reading through several solutions, this is the first one that really helped it click for me. Thanks.
Hm, the "Notice that ..." seems incomplete.
Log in to reply
I see, sorry, my fault. (I think) Now it is complete...
Excellent answer!
Great answer
The exterior angles of a polygon add up to 360 degrees. Therefore each exterior angle of a regular pentagon is 72 degrees. This 72 degrees is the base angle of each of the isosceles triangles making the points. This leaves 36 degrees for each point, totaling 180 degrees for all the points.
Même chose en français: les 5 sommets du pentagone sont inscrits dans un cercle. Cela fait 5 arcs de cercle qui les rejoignent. Chaque arc de cercle décrit un angle "au centre" de 360/5 = 72°. Or chaque sommet du pentagone opposé à un arc de cercle décrit donc un angle égal à la moitié de l'angle au centre soit 72 / 2 = 36°. La somme des angles des 5 sommets du pentagone fait donc 5 x 36 = 180°.
ΕΑch angle of the pentagram equal to 180- 360/5=72.so the trianleis isosceles so 180-(72+72)=36 36*5=180
My pen rotated twice going around the 5 outside angles, so each outside angle = 720/5 = 144. So each inner angle = 36...
Please expand on how you do that. This seems cool and very practical
How on earth do you figure out that your pen turns exactly twice?
Whats happening?.............please elaborate
Explain please
What do you mean?
For anyone in the future, this is a joke, please don
I will just leave this here. Meme question, but the star does not even have to be regular
We have 5 of the red quadrilaterals in the star. Each red quadrilateral has 3 of the blue angles. That is total 15 blue angles. 5 blue angles make the total internal angle of a regular pentagon, which is ( 5 − 2 ) × 1 8 0 ∘ = 5 4 0 ∘ . We are looking for the sum of the black angles, and we have 5 of them in 5 red quadrilaterals. S u m o f b l a c k = 5 × i n t e r n a l a n g l e s o f a q u a d r i l a t e r a l − 1 5 × b l u e a n g l e s . = 5 × 3 6 0 ∘ − 1 5 × ( 5 4 0 ∘ ) / 5 = 1 8 0 ∘ .
যেহেতু পঞ্চভুজ, তাই পাঁচ কোণের সমষ্টি = (n-2)180 degree = (5-2)180 degree = 540 degree. “ত্রিভুজের যেকোনো বহিস্থ কোণ বিপরীত অন্তস্থ কোণদ্বয়ের সমষ্টির সমান” - উপপাদ্য ব্যবহার করে দেখানো যায়, প্রতিটি কোণ 36 degree(180-72 × 2), অর্থাৎ 36 × 5 = 180 degree. )
Let the circle be divided by 5 so, that's (360/5=72) which will be the the angle of the intercepted arc. Then an inscribed angle is half of the angle of the intercepted arc so, (72/2=36). Then, the sum of internal angles is (36x5=180)
The internal angles of a n-gon sums 180° (n - 2). Then each internal angle of the pentagon is 108°, if we take the pentagon and glue one of the triangles creating a quadrilateral, 3 of the angles will be 108°, their internal angles should sum 360°, so the other angle should be 36°. The answer is 36°(5)
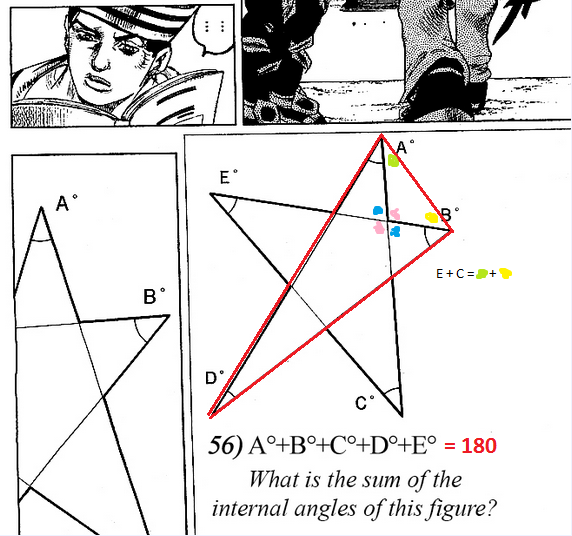
Imagine a stick lying along one of the stars lines and rotating through each angle in turn. It makes a total of one-half rotation and ends up at the original line, pointing in the opposite direction. So the sum of the angles is 180, and it doesn't matter if the star is irregular.
-
-
We know that the sum of the angles in a triangle is 180 degrees, it gives:
- a+d+E=180 or as we will use later E=180-a-d
- e+b+A=180
- d+b+C=180
-
e+c+D=180
-
We can also find the angle b by
-
k+m+b=180 so b=180-k-m
-
We also know that k+D=180 so k=180-D
- and m+E=180 so m=180-E
- Now we can find be with D and E
- 180-(180-D)-(180-E)=b
- D-180+E=b
-
D=b-E+180
-
180=180 so
- e+c+D=a+d+E
-
D-E=a+d-e-c
-
So
- b-E+180-E=a+d-e-c
- 180-2E=a+d-b-e-c
- 180-2*(180-a-d)=a+d-b-e-c
- 180-360+2a+2d=a+d-b-e-c
- -180=-a-b-c-d-e
-
a+b+c+d+e=180
-
I think this proof will work for all the 5 pointed stars, not only the regulars.
Let the edges be A, B, C, D, E in counterwlockwise order. Thus we calculate : ( A C , A D ) + ( B D , B E ) + ( C E , C A ) + ( D A , D B ) + ( E B , E C )
By rearranging the terms and using the property ( u , v ) = ( − u , − v ) which is true for any two vectors, we get:
( A C , A D ) + ( A D , B D ) + ( B D , B E ) + ( B E , C E ) + ( C E , C A ) = ( A C , C A ) = 1 8 0 ∘
The external angle of any regular polygon is derived by the formula of 360/n where n is the number of sides. In this case we have the angle 72°. Taking a look at all the triangles we can see that they are congruent and isosceles. Thus the internal angle for the point is 36° and 36x5 is 180°.
Interior angle of pentagon is 108. Hence each outer triangle have have two base angles of 72 degree each and third angle will be of 36 degree. sum of internal angles of 5 points will be 36*5=180
internal angle of central pentagon is 108.hence the two equal angles of the isosceles triangle are(180-108=72).thus the third one is 180-2 72=36.therefore sum of the angles is 36 5=180
sorry 365 is actually 36*5
Let the edges be A,B,C,D,E and the triangles containing the edges be a,b,c,d,e. B+D = one non- vertice angle in triangle a. Similarly C+E = another non-vertice angle in triangle a. So A+B+C+D+E = sum of all angles in triangle a. Hence 180
each angle of pentagon=540/5,then,angle on the otherside in the pentagram triangle (linear pair),180-(540/2),this is twice in the same triangle so 2X of it then to find the respective andle=180 minus the 2X value and multiple it for the respective 5 pts' angle sum......finally ans=5(180-2(180-(540/5))
You can see an isosceles triangle with 108' and 36' stretching from angle of pentagon and angle of pentagram.
5 X 36' = 180'
internal angle in a pentagon is 108.anlle of a straight line is 180.angle of one side of traingle is 180-108=72.star angle of a triangle is 180-144=36.so 36*5=180.
Make the outer circle through all stars' peaks and center in the middle of the chevron. internal angle is half of the central angle which is 360 divided by 5 = 72 --> internal angle is 36. So the sum of all internal angles is 5x36 = 180
i took ideal angular results for regular pentagon internal angles i. e. 108 deg
then i found external angles of this pentagon which are =180-108 =72 deg
now as the sum of angles of a triangle is 180 always and these all are iso-scales triangles we come to know that internal angle of pentagram is 36 deg
thus, add up all 5 angles to get 5* (36) = 180 deg
j o i n a l l p o i n t s t o f o r m a c i r c l e N o w c o n c i d e r o n e i n t e r n a l a n g l e t h e a r c w h i c h s u b t e n d i t . I n t o t a l t h e r e a r e 5 o f t h i s a r c , j o i n e d e n d t o e n d w h i c h w i l l s u b t e n d a t o t a l o f 3 6 0 i n c e n t r e S o 7 2 0 s u b t e n d e d b y o n e a r c i n c e n t r e , S o a n g l e a t c i r c u m f e r e n c e = 7 2 / 2 = 3 6 d e g r e e = i n t e r n a l a n g l e = 3 6 d e g r e e S o 5 i n t e r n a l a n g l e = 1 8 0 d e g r e e
each angle of pentagon is 72degs.this equal to sum of two opposite angles of atriangle.since both angles <vertex/&opposite angle are equal,so verteqx is 36 degs.thus sum of 5 vertex angles is 5x36=180
Log in to reply
what triangle are you talking about? from the next time be specific
since bothanglesare equal so vertex is 36 degs.so sum ofall vertexes is 5x36=180
Consider the pentagon within the given star.
Since it's a sided polygon then the sum of its interior angles is ( 5 − 2 ) 1 8 0 ∘ = 5 4 0 ∘ .
So let's say one of its angle is 5 5 4 0 º = 1 0 8 ∘ .
Using property of linearity you will find that corner angle is 3 6 ∘ .
So 3 6 ∘ × 5 = 1 8 0 ∘ .