Star Study - Integral Angles
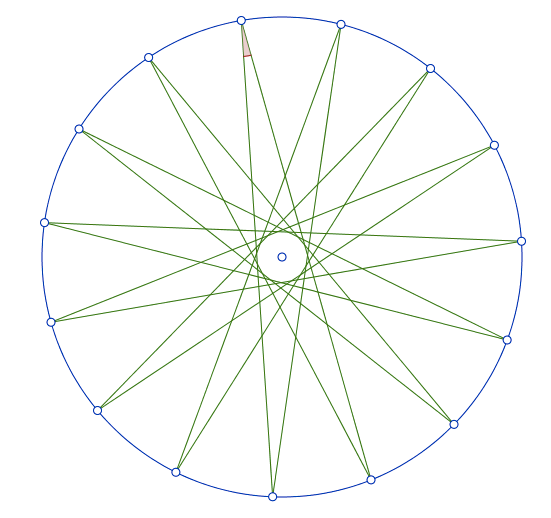 Take
n
points that are equally spaced on the circumference of a circle. For each point, connect it to the 2 points that are furtherest away from it, but not diametrically opposite to it. This forms an
n
pointed star.
Take
n
points that are equally spaced on the circumference of a circle. For each point, connect it to the 2 points that are furtherest away from it, but not diametrically opposite to it. This forms an
n
pointed star.
For how many integers n ≥ 5 is the measure (in degrees) of an individual internal angle in an n pointed star also an integer?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Ah, I forgot to subtract the values lower than 5 for the even star.
i dont understand the question~lol~
But in the condition it's note that n is greater or equal of 5? I think, that correct answer is 20?Is there some regular polygon for which the discovering measure is integer but the number of vertices is not from the set of divisors?
Indeed, the answer should be 20. I accidentally added in 2, 4 in the even case.
The problem has been updated.
The question is confusing man
From the question I assume that n can only be odd, as the formulation of the question says "For each point, connect it to the 2 points that are furtherest away from it, but not diametrically opposite to it" and that means (from my understanding) that you can only have odd number of points in the star... If n is even you will have a furtherer point that is the diametrically opposit, wich the formulation says you cannot use.
i actually have a doubt sir for n belongs to even integers the measure of the angle will get 2 * 360/n ( because we dont take diametrically opposite points) so the measure of angle is doubled and another set of values is added like 720 , 144, 48 ,16,80,
Tricky problem. This will work with odd or even values of n. For a star with an even number of points, draw from one point to the opposite side of the circle, but connect to the two points on either side of the point directly opposite. The angle drawn will create an inscribed angle on one side of the circle, connected to two points (separated by one) on the other side of the circle. The arc between those two points will be twice the length of 360/n. So, this means that the inscribed angle on the other side of the circle (the point of the star) would have a measure of...
2 ( 2 n 3 6 0 )
which can be stated as...
n 3 6 0
For a star with an odd number of points, there won't be a point separating the two points that form the central angle (since you can draw directly to two points that are not diametrically opposite), so the measure of the arc (and the central angle) connecting those two points would be 360/n. The inscribed angle opposite (the point of the star) would have a measure of...
2 ( n 3 6 0 )
which can be stated as...
n 1 8 0
My understanding is that the question is asking how many stars of n ≥ 5 points will have individual internal angles that are integers (whole numbers).
So, which values of n go into 360 or 180 evenly? So, I found the factors of 360... 1,2,3,4,5,6,8,9,10,12,15,18,20,24,30,36,40,45,60,72,90,120,180,360 ... and removed 1-4 since you can't make a star with this many points. 20 values of n.
Note: I came to this the looong way, after first making a table where I calculated every internal angle between n=5 and n=36 and circle the values that were integers.
If n is odd, we have a sum of 1 8 0 ∘ , so we want all odd divisors of 1 8 0 . We have 1 8 0 = 2 2 × 3 2 × 5 so we actually want all divisors of 3 2 × 5 = 4 5 . That is, 5 , 9 , 1 5 , 4 5 .
If n is even, we have a sum of 3 6 0 ∘ , so we want all even divisors of 3 6 0 = 2 3 × 3 2 × 5 . We can do this by counting all divisors of 3 6 0 and subtracting all odd ones (or ≤ 5 ). 3 6 0 has 4 × 3 × 2 = 2 4 divisors (powers of prime numbers, added one and multiplied together), while the 'odd part' of 3 6 0 (i.e. 4 5 ) has 4 divisors greater than 5 , so we're left with 2 4 − 4 = 2 0 . Now we subtract the small ones, that is 1 , 2 , 3 , 4 and we get 1 6 divisors.
We add 4 + 1 6 and we get 2 0 . We look at the possible answers and we guess it must be 22. (We actually get 22 if we add the cases when n < 5 , that is n = 4 and n = 3 , so I'm assuming that's why the answer is 22.)