Star Study - n pointed total
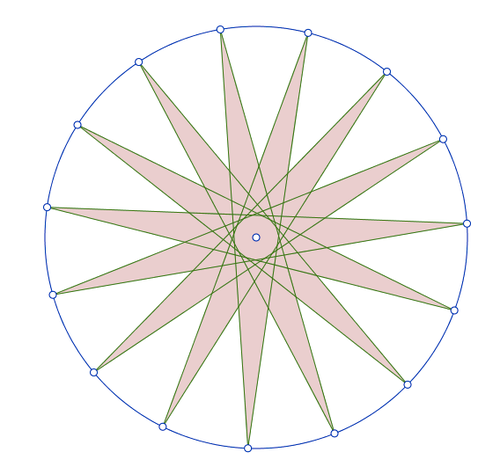 Take
points that are equally spaced on the circumference of a circle. For each point, connect it to the 2 points that are furtherest away from it, but not diametrically opposite to it. This forms an
pointed star.
Take
points that are equally spaced on the circumference of a circle. For each point, connect it to the 2 points that are furtherest away from it, but not diametrically opposite to it. This forms an
pointed star.
What is the sum of the internal angles (in degrees)?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Because each internal angle of n-pointed star is equal to haft of in-center angle with the same arc. If n is odd, these in-center angles are separated and cover whole circle, so sum of them is: 3 6 0 0 Hence sum of internal angles of n-pointed star is: 1 8 0 0 If n is even, these in-center angles pairwise overlap each other in haft of each. So sum of these angles is: 3 6 0 × 2 = 7 2 0 0 So sum of internal angles of n-pointed star is: 3 6 0 0 Answer is: 1 8 0 0 : n = 2 k + 1 , 3 6 0 0 : n = 2 k