Stars Within Stars

Geometry Level 4

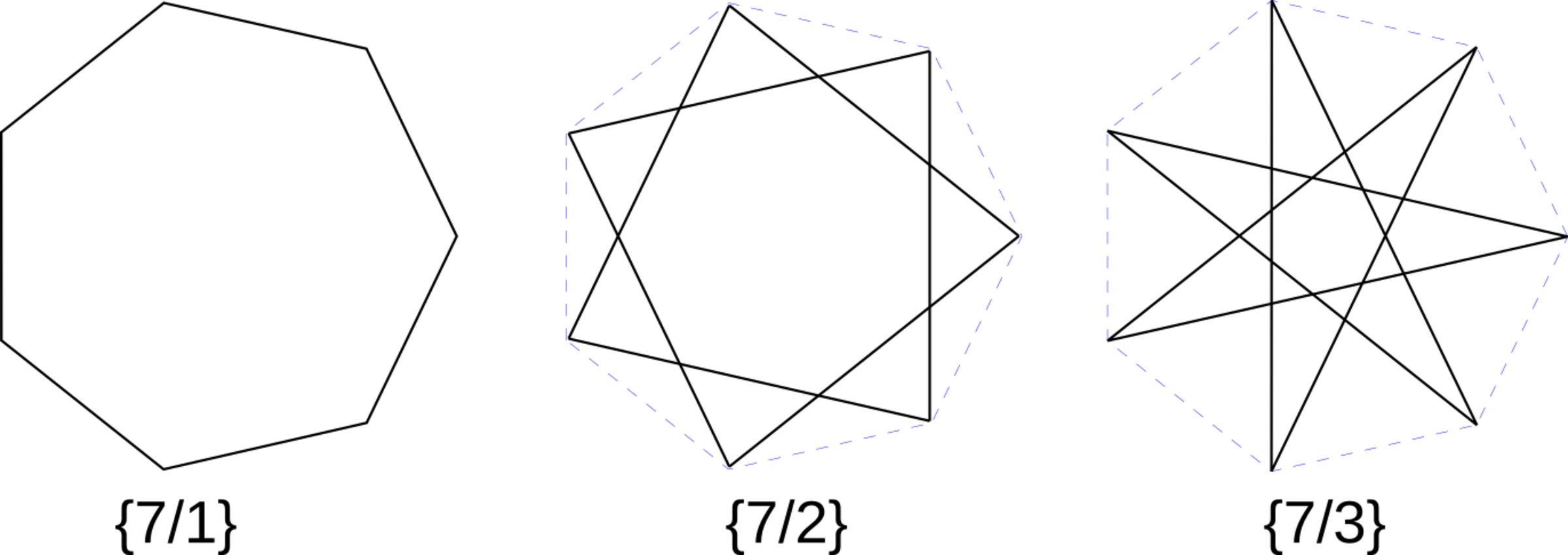
Let $\{p/q\}$ denote the $p$ -pointed star formed by joining every $q^{\text{th}}$ vertex on a convex $p$ -gon until you reach the starting point. This is repeated with different starting points if necessary until we form a $p$ -pointed star.

Is it true that $\{p/q\}$ contains $\{p/r\}$ if $r \le q$ ?

Note:

$\{p/q\}$ is defined for all $p \ge 3$ , and $1 \le q < \frac p2$ .
As an explicit example, the following shows three possible $7$ -pointed stars. Here $\{7/2\}$ contains $\{7/1\}$ because there is an instance of $\{7/1\}$ inside $\{7/2\}$ .

Yes, it holds for all

p

No, it holds only for certain

p

No, it does not hold for any

p

1 solution

Marta Reece
Apr 28, 2017

Star polynomial connecting the original, black, points skips $q-1$ points as it goes around, in this case four.

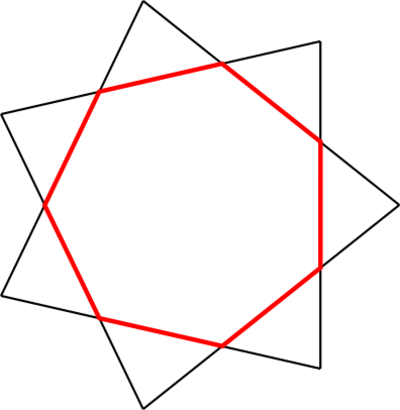
The first intersections inward from there, red points in the image, are equal in number, but they are located between the black points and the star polynomial connecting them skips one fewer points, in this case three.

Next set of intersections, blue in the image, contains again the same number of points but their connection skips only two, etc. all the way to skipping none at all.

This construction can be done for any $p$ , with each layer inward having $q$ one smaller than the previous one, so no $q$ will be skipped and all $\{p, r\}$ combinations with $r<q$ will be present, as well as the original $q$ , of course.

Stars Within Stars

1 solution

0 pending reports