Static Charged Particles on a Wire

Electricity and Magnetism Level 3

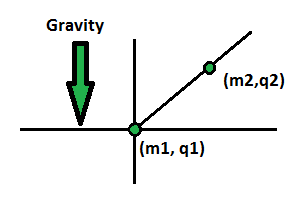
In the $xy$ -plane, there is a semi-infinite wire in the shape of the curve $y = x$ .

Particle 1, with mass and charge $\big(m_1 = 0 \text{ kg}, q_1 = +10^{-4} \text{ C}\big)$ , is fixed at the origin.
Particle 2, with mass and charge $\big(m_2 = 1 \text{ kg}, q_2 = +10^{-4} \text{ C}\big)$ , can slide freely along the wire.

There is a uniform downward gravitational acceleration $g = \SI[per-mode=symbol]{10}{\meter\per\second\squared}$ .
The Coulomb constant is $k_e = \SI[per-mode=symbol]{9e9}{\newton\meter\squared\per\coulomb\squared}$ .

If Particle 2 is in static equilibrium, what is the $x$ -coordinate of its position (in meters, to 2 decimal places)?

The answer is 2.52.

1 solution

Prakhar Bindal
Nov 19, 2016

Equate the force due to gravity and the electrostatic force of repulsion along the line y=x

Let the position of particle is (x,x)

kq1q2/2x^2 = 10*sin(45)

from here x = 3/2^(0.25)

Static Charged Particles on a Wire

The answer is 2.52.

1 solution

0 pending reports