Statics Exercise (11/16/2017)

Let $R_{\parallel}$ and $R_{\perp}$ be the components of the reaction force, $R$ , at $P$ , parallel and perpendicular to the rod, in Newtons. Let $T_{\parallel}$ and $T_{\perp}$ be the components of the tension in the rope, $T$ , parallel and perpendicular to the rod, in Newtons. Let $\theta$ be the angle the rope makes with the rod, and $l$ be the length of the rope, in meters. Considering the triangle containing the rope and point $P$ . By the cosine rule

$l^2 = \left(\frac{1}{2}\right)^2 + \left(\frac{1}{3}\right)^2 - 2 \frac{1}{2} \frac{1}{3} \cos 60^\circ$

$\Rightarrow l = 0.441$

Then, by the sine rule,

$\frac{\sin \theta}{1/2} = \frac{\sin 60^\circ}{0.441}$

$\Rightarrow \theta = 79.11^\circ$

Forces parallel and perpendicular to the rod must balance:

$g \sin 60^\circ + T_{\parallel} = R_{\parallel}$

$g \cos 60^\circ + T_{\perp} = R_{\perp}$

The center of mass of the rod is 1/6 m from $P$ . Moments must also balance:

$\frac{1}{6} g \cos 60^\circ = \frac{1}{3} T_{\perp}$

$\Rightarrow T_{\perp} = 2.5$

Then

$T_{\parallel} = \frac{ T_{\perp} }{\tan 79.11^\circ}$

i.e. $T_{\parallel} = 0.481,$

so that $R_{\perp} = 7.5, R_{\parallel} = 9.14,$ and $R = \sqrt{R^2_{\perp} + R^2_{\parallel}}$

i.e. $R = 11.82$ .

There are three forces acting on the stick: the weight $W$ , the reaction force $R$ , and the tension force $T$ .

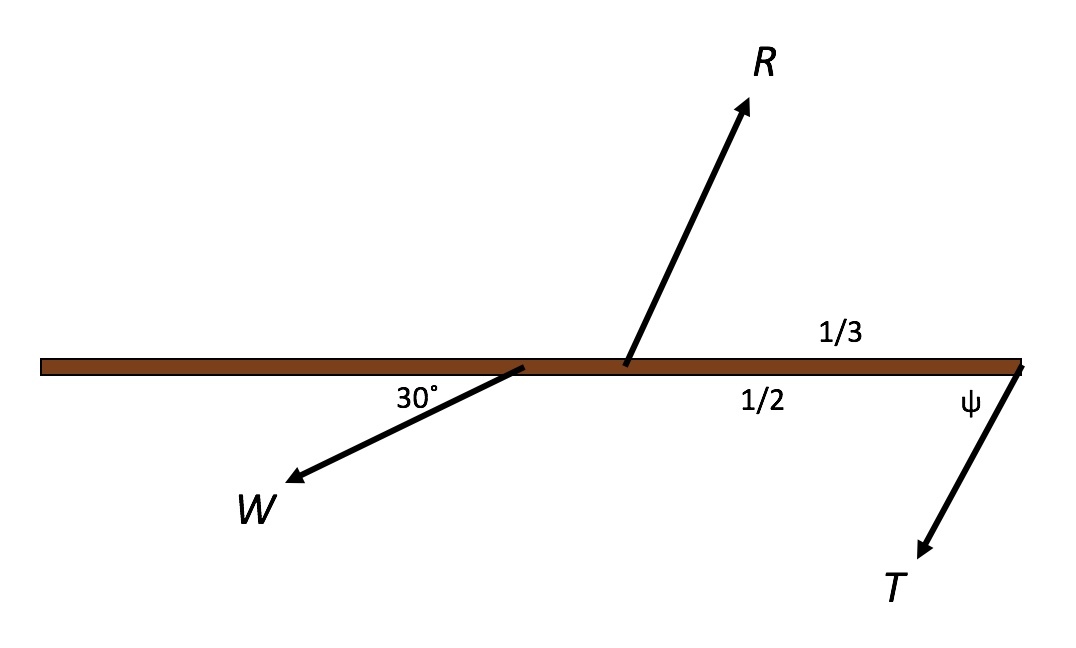
First some geometry

To find the direction of the tension force, consider that the stick overhangs the table by $\tfrac13\cos 60^\circ = \tfrac 16$ . Thus the horizontal extent of the rope is $\tfrac 12 - \tfrac 16 = \tfrac 13$ . The vertical extent of the rope is $\tfrac13\sin 60^\circ = \tfrac16\sqrt 3$ . Thus the direction angle $\theta$ between table and rope satisfies $\tan \theta = \tfrac 16\sqrt 3 / \tfrac 13 = \tfrac 12\sqrt 3$ .

Now consider the triangle formed by the stick, rope, and table. For the angle between rope and stick $\psi$ we have $\psi = 180^\circ - 60^\circ - \theta$ , so that $\tan \psi = -\tan (60^\circ + \theta)$ : $\frac{T_y}{T_x} = -\tan (60^\circ + \theta) = -\frac{\tan 60^\circ + \tan \theta}{1 - \tan 60^\circ\tan \theta} = -\frac{\sqrt 3 + \tfrac12\sqrt 3}{1 - \sqrt 3\cdot \tfrac12\sqrt 3} = 3\sqrt 3.$

Analyzing the equilibrium

Equilibrium of forces and torques (relative to the top of the stick) requires $R_x = W_x + T_x \\ R_y = W_y + T_y \\ \tfrac13 R_y = \tfrac12 W_y.$ Starting with the bottom equation, $R_y = \tfrac 32 W_y = \tfrac 34 W.$ The middle equation gives $T_y = R_y - W_y = \tfrac 34 W - \tfrac 12 W = \tfrac14 W.$ From our geometry investigation we have $T_x = \frac{T_y}{3\sqrt 3} = \tfrac 1{36}\sqrt 3 W.$ The first equation then shows $R_x = W_x + T_x = \tfrac12\sqrt 3 W + \tfrac1{36}\sqrt 3 W = \tfrac{19}{36}\sqrt 3 W.$ Pythagoras tells us $R = \sqrt{R_x^2 + R_y^2} \approx 1.1824W = \boxed{\SI{11.82}{N}}.$