Statics with Trigonometry!
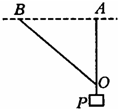 As shown in the figure, the
non-stretch light rope
and
are attached to a node
,
is attached to an object
,
, where point
and
are fixed on the same horizontal line. At the beginning,
is vertical and the two ropes are just stretched. The tensions of
and
are denoted as
and
respectively. Now, keeping
and
on the same horizontal line, if we
slowly
move point
to the left
, what can we say about
and
as
increases?
As shown in the figure, the
non-stretch light rope
and
are attached to a node
,
is attached to an object
,
, where point
and
are fixed on the same horizontal line. At the beginning,
is vertical and the two ropes are just stretched. The tensions of
and
are denoted as
and
respectively. Now, keeping
and
on the same horizontal line, if we
slowly
move point
to the left
, what can we say about
and
as
increases?
Note: Can you rigorously prove it?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Fb * cosθ = Fa * cosα
and
Fb*sinθ +Fa *sinα =G
So we will get Fa =G * s i n ( θ + α ) c o s θ
Then its first order derivation of θ is Fa' {θ} =G * s i n 2 ( θ + α ) − c o s ( α ) which 0<2θ+α<1.5π and its first order derivation of α is Fa' {α} = G * s i n 2 ( θ + α ) − c o s θ ∗ c o s ( θ + α ) 0<θ<0.5π 0<θ+α<π
So Fa' {θ}<0 all the time
We can know that at first 0.5π<θ+α.hence, Fa' {α}>0. And | Fa' {θ}|>|Fa' {α}|
Gradually,it becomes 0<θ+α<0.5π,which makes Fa'_{α}<0.
As a result , we can know that Fa decreases ,and then increases