Stationary point between sun and earth

The earth orbits the sun sun in a distance $a$ with the angular velocity $\Omega = 2 \pi / \text{year}$ . For this orbit, the gravitational force of the sun and the centrifugal force must be in balance: $\begin{aligned} F_g = \frac{G M_E M_S}{a^2} &= M_E \Omega^2 a = F_\text{cf} \\ \Rightarrow \quad \Omega^2 &= \frac{G M_S}{a^3} \end{aligned}$ The spacecraft orbits the sun at the same angular velocity $\Omega$ , so that it remains static relative to the sun and earth. The sun and the earth exert gravitational forces on the spacecraft. In addition, the centrifugal force acts on the spacecraft. In equilibrium $\begin{aligned} & & F_g &= F_\text{cf} \\ \Rightarrow & & \frac{G m M_S}{(a-x)^2} - \frac{G m M_E}{x^2} &= m \Omega^2 (a - x) = \frac{G m M_S}{a^3} (a -x) \end{aligned}$ Assuming that the distance $x$ is small compared to the Sun-Earth distance ( $x \ll a$ ), we can make a linear Taylor expansion of the 1st term: $\begin{aligned} & & \frac{1}{(a - x)^2} &\approx \frac{1}{a^2} + 2 \frac{x}{a^3} + \mathcal{O}\left( \frac{x^2}{a^2} \right)\\ \Rightarrow & & \frac{G m M_S}{a^2} + 2 \frac{G m M_S x}{a^3} - \frac{G m M_E}{x^2}& \approx \frac{G m M_S}{a^3} (a -x) \\ \Rightarrow & & \frac{3 G m M_S}{a^3} x &\approx \frac{G m M_E}{x^2} \\ \Rightarrow & & x &\approx \sqrt[3]{\frac{M_E}{3 M_S}} \cdot a \\ & & &\approx \sqrt[3]{\frac{1}{999,000}} \cdot a \approx \sqrt[3]{10^{-6} } \cdot a = 10^{-2} \cdot a = 1.5 \cdot 10^6 \,\text{km} \end{aligned}$

The spacecraft is at the Sun and Earth's first Lagragian Point , whose location is defined by

$\frac{M_1}{(R - r)^2} = \frac{M_2}{r^2} + \frac{M_1}{R^2} - \frac{r(M_1 + M_2)}{R^3}$

where $r$ is the distance of the point from the smaller object, $R$ is the distance between the two main objects, and $M_1$ and $M_2$ are the masses of the large and small object, respectively. In this problem, $r = x$ , $R = a = 150 \cdot 10^6$ km, and $M_1 = 333000M_2$ , so

$\frac{333000M_2}{(150 \cdot 10^6 - x)^2} = \frac{M_2}{x^2} + \frac{333000M_2}{(150 \cdot 10^6)^2} - \frac{x(333000M_2 + M_2)}{(150 \cdot 10^6)^3}$

which solves to $x \approx 1495480$ km or $x \approx \boxed{1.5} \cdot 10^6$ km

As David Vreken already stated, the point asked for is a Lagrangian Point . But how can we find it?

We start with the Lagrangian of a three-body system, which is the difference of the kinetic and the potential energies,

$\mathfrak{L}(\vec{r}, \vec{R}_1, \vec{R}_2) = \frac{m}{2} \dot{\vec{r}}^2 + \frac{M_1}{2} \dot{\vec{R}}_1^2 + \frac{M_2}{2} \dot{\vec{R}}_2^2 + G \frac{m M_1}{\left| \vec{r} - \vec{R}_1 \right|} + G \frac{m M_2}{\left| \vec{r} - \vec{R}_2 \right|} + G \frac{M_1 M_2}{\left| \vec{R}_1 - \vec{R}_2 \right|} ,$

where the $M_1 > M_2 \gg m$ are the masses of the three bodies (i.e. sun, earth and an object with negligible mass compared to the former) sitting at positions $\vec{R}_1$ , $\vec{R}_2$ and $\vec{r}$ . $G$ is the gravitational constant and $~\cdot~$ denotes the time derivative, that is, $\dot{\vec{r}} = \vec{v}$ is the velocity of the object at position $\vec{r}$ .

As we all know, the earth is traveling around the sun. In fact, the sun is also moving, since both objects are rotating around their center of mass (CM). Therefore, it is convenient so switch into the rotating frame, that is, the coordinate system which is rotating with the same angular velocity $\omega$ (see below).

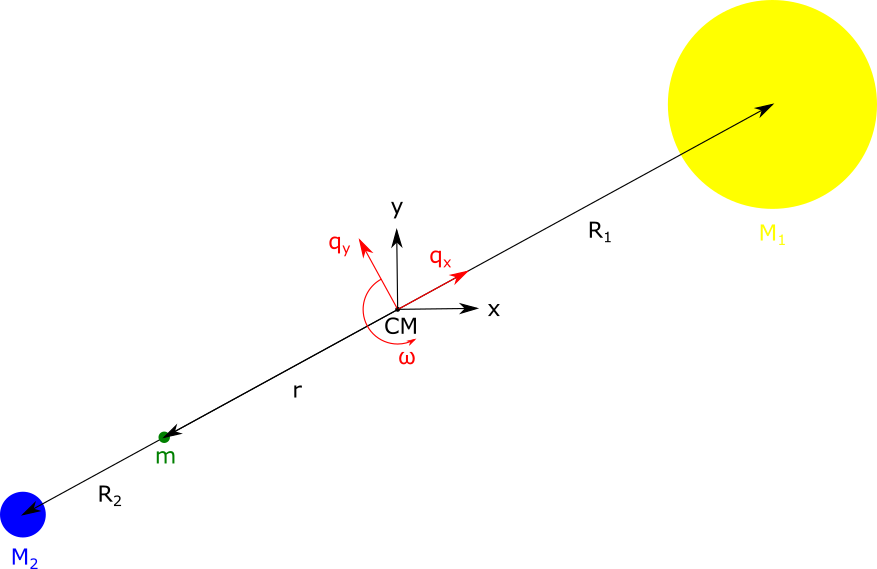The three-body problem: Two objects with masses $M_1$ and $M_2$ are rotating around their center of mass (CM) at angular velocity $\omega$ . The third object is a probe with negligible mass $m \ll M_1, M_2$ . The cartesian coordinates are given by $(x, y)$ . The rotating frame is given by $(q_x, q_y)$ .

The transformation between the coordinates $(x, y)$ and $(q_1, q_2)$ is given by a rotation

$\begin{aligned} x &= q_x \cos \omega t + q_y \sin \omega t , \\ y &= -q_x \sin \omega t + q_y \cos \omega t . \end{aligned}$

With some calculation we find that

$\begin{aligned} \left| \vec{r}_i - \vec{r}_j \right| &= \sqrt{\left( x_i - x_j \right)^2 + \left( y_i - y_j \right)^2} \\ &= \sqrt{\left( q_{x, i} - q_{x, j} \right)^2 + \left( q_{y, i} - q_{y, j} \right)^2} \\ &= \left| \vec{q}_i - \vec{q}_j \right| \end{aligned}$

and

$\begin{aligned} \dot{\vec{r}}_i^2 &= \dot{x}^2 + \dot{y}^2 \\ &= \dot{q}_{x, i}^2 + \dot{q}_{y, i}^2 + \omega^2 \left( q_{x, i}^2 + q_{y, i}^2 \right) + 2 \omega \left( \dot{q}_{x, i} q_{y, i} - q_{x, i} \dot{q}_{y, i} \right) \\ &= \dot{\vec{q}}_i^2 + \omega^2 \vec{q}_i^2 + 2 \omega \dot{\vec{q}}_i \times \vec{q}_i . \end{aligned}$

Note: Multiplication of the last line by a mass and division by two (that is how they appear in the Lagrangian) we find some familiar terms. The first term is simply the kinetic energy in the rotating frame. The second term is the centrifugal force , an fictitious force felt by a rotating observer. The last term is the Coriolis force , another fictitious force.

To make life easier, we will make some simplifications before plugging these results into the Lagrangian. Since the masses $M_1$ and $M_2$ are rotating around the CM, we can fix them to the $q_x$ -axis in the rotating coordinate system, i.e. $Q_{y, 1} = Q_{y, 2} = 0$ and $\dot{Q}_{y, 1} = \dot{Q}_{y, 2} = 0$ . Since the (Lagrangian) point we are looking for is on the line connecting $M_1$ and $M_2$ , the same holds for the object of mass $m$ : $q_y = \dot{q}_y = 0$ .

Now, the Lagrangian in terms of the rotating coordinates and corresponding to the given problem reads

$\mathfrak{L}(q_x, Q_{x, 1}, Q_{x, 2}) = \frac{m}{2} \dot{q}_x^2 + \frac{m \omega^2}{2} q_x^2 + \frac{M_1}{2} \dot{Q}_{x, 1}^2 + \frac{M_1 \omega^2}{2} Q_{x, 1}^2 + \frac{M_2}{2} \dot{Q}_{x, 2}^2 + \frac{M_2 \omega^2}{2} Q_{x, 2}^2 + G \frac{m M_1}{\left| q_x - Q_{x, 1} \right|} + G \frac{m M_2}{\left| q_x - Q_{x, 2} \right|} + G \frac{M_1 M_2}{\left| Q_{x, 1} - Q_{x, 2} \right|} .$

The equations of motion for $m$ , $M_1$ and $M_2$ can be calculated via the Euler-Lagrange equations , which yields

$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{\partial \mathfrak{L}}{\partial \dot{q}_x} \right) = m \ddot{q}_x &= m \omega^2 q_x + G \frac{m M_1 \left( q_x - Q_{x, 1} \right)}{\left| q_x - Q_{x, 1} \right|^3} + G \frac{m M_2 \left( q_x - Q_{x, 2} \right)}{\left| q_x - Q_{x, 2} \right|^3} = \frac{\partial \mathfrak{L}}{\partial q_x}, \\ \frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{\partial \mathfrak{L}}{\partial \dot{Q}_{x, 1}} \right) = M_1 \ddot{Q}_{x, 1} &= M_1 \omega^2 Q_{x, 1} - G \frac{m M_1 \left( q_x - Q_{x, 1} \right)}{\left| q_x - Q_{x, 1} \right|^3} + G \frac{M_1 M_2 \left( Q_{x, 1} - Q_{x, 2} \right)}{\left| Q_{x, 1} - Q_{x, 2} \right|^3} = \frac{\partial \mathfrak{L}}{\partial Q_{x, 1}} , \\ \frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{\partial \mathfrak{L}}{\partial \dot{Q}_{x, 2}} \right) = M_2 \ddot{Q}_{x, 2} &= M_2 \omega^2 Q_{x, 2} - G \frac{m M_2 \left( q_x - Q_{x, 2} \right)}{\left| q_x - Q_{x, 2} \right|^3} - G \frac{M_1 M_2 \left( Q_{x, 1} - Q_{x, 2} \right)}{\left| Q_{x, 1} - Q_{x, 2} \right|^3} = \frac{\partial \mathfrak{L}}{\partial Q_{x, 1}} . \end{aligned}$

Since we assumed that $M_1$ and $M_2$ , i.e. the sun and the earth, are rotating with angular velocity $\omega$ , their orbits should be stable and their centripetal forces should match the gravitational force. In that case, $\ddot{Q}_{x, 1} = \ddot{Q}_{x, 2} = 0$ . Furthermore, we are looking for the point where any object of mass $m$ is stationary as well, such that $\ddot{q}_x = 0$ .

By indentifying $a = Q_{x, 1} - Q_{x, 2}$ , $x = q_x - Q_{x, 2}$ and $a - x = Q_{x, 1} - q_x$ we obtain

$\frac{M_1}{\left( a - x \right)^2} = \frac{M_2}{x^2} + \frac{\omega^2}{G} q_x$

from the first line, which is independent of the mass $m$ . Analogously we find

$\begin{aligned} - \frac{\omega^2}{G} Q_{x, 1} &= \frac{M_2}{Q_{x, 2}} + \underbrace{\frac{m}{x^2}}_{\approx 0} , \\ \frac{\omega^2}{G} Q_{x, 2} &= \frac{M_1}{Q_{x, 1}} + \underbrace{\frac{m}{\left( a - x \right)^2}}_{\approx 0} \end{aligned}$

from the second and third lines, respectively. Since the mass $m$ is negligible in comparison with $M_1$ and $M_2$ , we can neglect the last terms.

The second equation gives us an expression for $Q_{x, 2}$ (which we will need in a moment),

$Q_{x, 2} = - \frac{M_1}{M_1 + M_2} a ,$

and adding both equations and dividing by $a$ gives us an expression for $\omega$ ,

$\frac{\omega^2}{G} = - \frac{M_1 + M_2}{a^3} .$

Now we can plug this relation into the equation above (the one obtained from the equation of motion for $q_x$ ):

$\frac{M_1}{\left( a - x \right)^2} = \frac{M_2}{x^2} - \frac{M_1 + M_2}{a^3} q_x = \frac{M_2}{x^2} - \frac{M_1 + M_2}{a^3} Q_{x, 2} - \frac{M_1 + M_2}{a^3} x .$

With the relation for $Q_{x, 2}$ we calculated above we finally obtain

$\frac{M_1}{\left( a - x \right)^2} = \frac{M_2}{x^2} + \frac{M_1}{a^2} - \frac{M_1 + M_2}{a^3} x ,$

which is a fifth order equation for $x$ . Thus, without approximations we cannot determine $x$ analytically.

Note: In contrast to the two-body problem, the three-body problem is analytically not solvable anymore.

By setting $M_1/M_2 = M_S/M_E = 333,000$ and $a = 150\,\mathrm{Gm}$ we can solve

$\frac{1}{x^2} + \frac{M_1}{M_2} \frac{1}{a^2} - \left( \frac{M_1}{M_2} + 1 \right) \frac{x}{a^3} - \frac{M_1}{M_2} \frac{1}{\left( a - x \right)^2} = 0$

numerically with ease. Using Newton's method we find $x \approx 1.4954798969543903\,\mathrm{Gm}$ .