Stationary Stone Bar
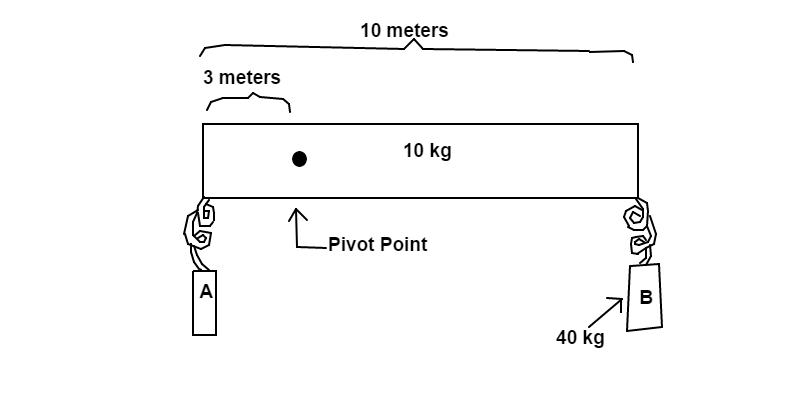
A uniform stone bar with a mass of 1 0 kg and a length of 1 0 m has a pivot point that is 3 m away from the nearest edge. Two weights, A and B , are hung onto the edges of the bar by massless springs where weight B is hung on the edge farthest from the pivot point. If the mass of weight B is 4 0 kg , what must the mass of weight A be to prevent the bar from turning?
Assume g = 9 . 8 1 s 2 m .
The answer is 100.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Why the d of the bar is 2m?
Log in to reply
The gravitational force from just the bar can be assumed to occur at the bar's center of mass. Because the bar is uniform, the center of mass would be at the center of the bar, which would be 5 m from the edges. Notice that the pivot point is 3 m from the nearest edge; thus the distance between the bar's downward gravitational force and the pivot point is 5 − 3 = 2 m . In the torque formula, d is the distance between the force being applied on an object and the pivot point of that object.
Just need to balance the torque on both the sides
On the right one of the torque is produced by
4
0
kg
which is
r
×
F
=
7
×
4
0
×
9
.
8
1
Plus torque due to weight of the rod which is intergration (
d
M
×
g
×
x
) where
d
M
is small mass of an element of length
d
x
and
x
is the distance of small mass from pivoted point.
d M = M / L = ( 1 0 k g / 1 0 m ) d x
Now just integrate from limit
x
=
0
t
o
7
and you'll get
g
(
x
2
)
/
2
where
x
=
7
and so total torque
=
(
4
9
g
/
2
)
+
7
×
4
0
×
g
You may neglect g on both sides as it will get cancel in the end
Now for right part just follow the same procedure
Total torque on left
=
3
m
g
+
∫
d
M
×
g
×
x
where
m
is mass of block A and
M
is total mass of rod and this time integrate
x
from
0
to
3
and put
d
M
as
(
1
0
/
1
0
)
d
x
and you'll get
3
m
g
+
(
9
g
/
2
)
Now cancel
g
(
4
9
/
2
)
+
2
8
0
=
3
m
+
(
9
/
2
)
So
m
=
1
0
0
kg
Thanks for sharing your approach, Saanika. I have edited the Latex so your solution is easier to read.
The total torque ( T ) experienced by the bar must be zero in order to prevent the bar from spinning. △ T = 0 s 2 k g ⋅ m 2 a n d T o b j e c t = F d sin ( θ ) T A = T b a r + T B ( 9 . 8 1 s 2 m ) ( 3 m ) ( m A ) sin ( 9 0 ∘ ) = ( 9 . 8 1 s 2 m ) ( 2 m ) ( 1 0 k g ) sin ( 9 0 ∘ ) + ( 9 . 8 1 s 2 m ) ( 7 m ) ( 4 0 k g ) sin ( 9 0 ∘ ) ( 3 m ) ( m A ) = 2 0 m ⋅ k g + 2 8 0 m ⋅ k g m A = 3 m 3 0 0 m ⋅ k g = 1 0 0 k g
N o t e : Because g was a common term in step ( 3 ) , I divided it out to simplify the math.