Steel Ball Drop
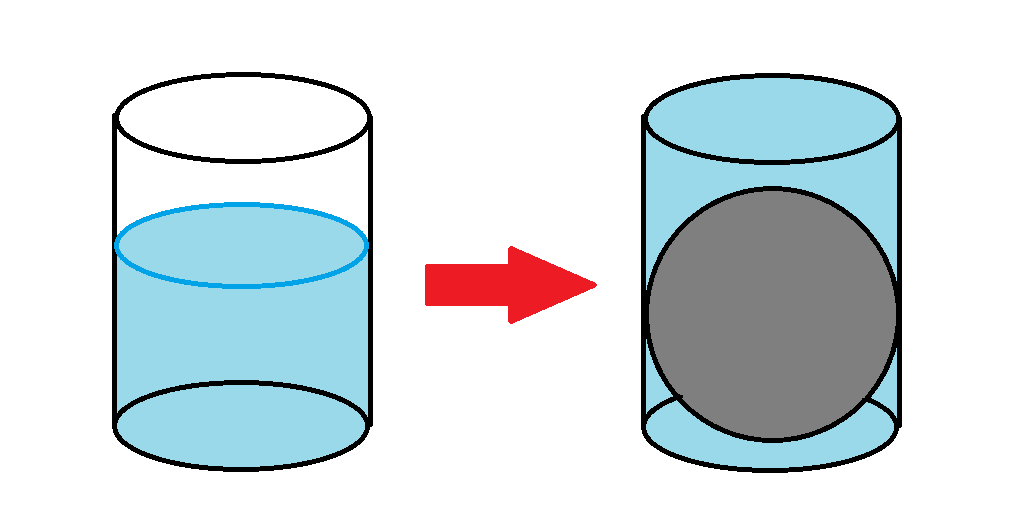
A cylindrical glass is partially filled with water at the same height as the diameter of its base. Then a spherical steel ball of the same diameter is dropped into the water, raising the water level by 4 cm up to the very top of the glass.
How high is this glass in cm?
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The volume of the steel ball equals to the cylindrical volume raised.
Thus, 3 4 π ( r 3 ) = π ( r 2 ) h = 4 π ( r 2 ) .
Hence, 3 r = 1 . r = 3 .
Finally, the glass's height = 2 × 3 + 4 = 1 0 .
You said finally twice, you can combine those last two sentences not to be rude or anything.
Let r be the radius of the cylinder and sphere. Then the initial height of water is h = d = 2 r . The volume of rise of water is equal to the volume of the sphere. So we have
π r 2 ( 4 ) = 3 4 π r 3
r = 3
So the height of the the glass is h + 4 = 2 r + 4 = 2 ( 3 ) + 4 = 6 + 4 = 1 0 .
Then,
V c = V w + V s
π r 2 ( h + 4 ) = π r 2 h + 3 4 π r 3
π r 2 ( h + 4 ) = π r 2 ( h + 3 4 r ) ⟹ π r 2 cancels out
h + 4 = h + 3 4 r ⟹ h cancels out
3 = r
but: h = 2 r ⟹ r = 2 h
therefore,
3 = 2 h
6 = h
Finally, the height of the cylinder is
h + 4 = 6 + 4 = 1 0 c m a n s w e r