Steiner’s December Triangle
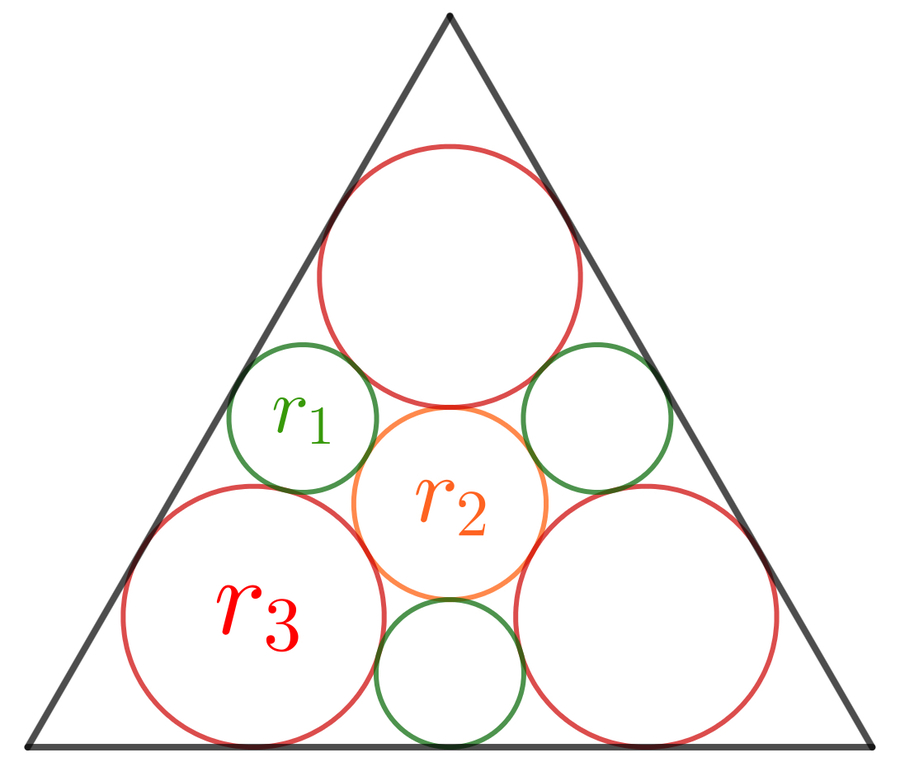
As shown in the figure, an equilateral triangle inscribes seven circles, three with a radius of r 1 , three with a radius of r 3 , and the central circle has a radius of r 2 .
If r 1 r 2 + r 3 = b a ( c + d e ) , where a , b , c , d , and e are positive integers with a and b being coprime and e square-free, find a + b + c + d + e .
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Michael Huang , you have to mention that the triangle is equilateral. If a and b are non-zero integers, then a = − 2 and b = − 3 are also valid solutions that a + b + c + d + e = 1 0 . I have amended the problem statement for you.
Since we're interested in ratios, we can take the side length of the triangle to be 1 . Then we can write the following three relations involving r 1 , r 2 and r 3
2 r 1 + r 2 = 2 3 1 ( 1 )
r 2 + 3 r 3 = 3 1 ( 2 )
( r 1 + r 3 ) 2 = ( r 1 − r 3 ) 2 + ( 3 r 3 − 2 1 ) 2 ( 3 )
Solving the first two equations, results in:
( r 1 , r 2 , r 3 ) = ( − 4 3 1 , 3 1 , 0 ) + t ( 2 3 , − 3 , 1 )
Pluggin this into equation (3), results in a quadratic equation in t , which solves to
t = 6 3 1 ( 1 3 − 2 )
The required ratio is r 1 r 2 + r 3 = − 4 3 1 + 2 3 t 3 1 − 2 t
Pluggin in the value of t we obtained into the above quotient, and simplifying, results in:
r 1 r 2 + r 3 = 3 2 ( 1 + 1 3 )
Hence, a = 2 , b = 3 , c = 1 , d = 1 , e = 1 3 , and this makes the answer 2 0
Let r 1 = 1 , r 2 = x , r 3 = y , and label the diagram as follows:
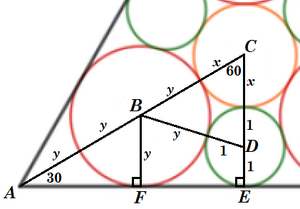
From right △ A B F we know that A B = cos 6 0 ° B F = 2 y .
From right △ A C E we know that A C = cos 6 0 ° C E = 2 x + 4 , and since A C = 3 y + x , 2 x + 4 = 3 y + x or x = 3 y − 4 .
By the law of cosines on △ B C D , B D 2 = B C 2 + C D 2 − 2 ⋅ B C ⋅ C D cos 6 0 ° , or ( y + 1 ) 2 = ( x + y ) 2 + ( x + 1 ) 2 − ( x + y ) ( x + 1 ) .
These two equations solve to x = 2 1 ( 1 3 − 1 ) and y = 6 1 ( 7 + 1 3 ) .
Therefore, r 1 r 2 + r 3 = 1 x + y = 3 2 ( 1 + 1 3 ) , so that a = 2 , b = 3 , c = 1 , d = 1 , e = 1 3 , and a + b + c + d + e = 2 0 .
Label the equilateral triangle A B C and the center of the central circle with radius r 2 be O . Due to symmetry, center O is also the centroid of △ A B C . Let the side length of △ A B C be 1 . Then A O = B O = C O = 3 1 and O N = 2 3 1 , where B N is a median of △ A B C . Then we have:
⎩ ⎪ ⎨ ⎪ ⎧ 3 r 3 + r 2 = 3 1 2 r 1 + r 2 = 2 3 1 . . . ( 1 ) . . . ( 2 ) ⟹ ( 1 ) − ( 2 ) : 3 r 3 − 2 r 1 = 2 3 1
Let the center of the left-bottom circle with radius r 3 be P and P M be perpendicular to A C . Then we have
A M + M N 3 r 3 + ( r 3 + r 1 ) 2 − ( r 3 − r 1 ) 2 3 r 3 + 2 r 1 r 3 2 r 1 r 3 4 r 1 r 3 1 6 r 1 r 3 8 ( 3 r 3 − 2 3 1 ) r 3 2 4 r 3 2 − 3 4 r 3 1 2 3 r 3 2 + 8 r 3 − 3 ⟹ r 3 r 2 r 1 ⟹ r 1 r 2 + r 3 = A N = 2 1 = 2 1 = 2 1 − 3 r 3 = 3 r 3 2 − 3 r 3 + 4 1 = 1 2 r 3 2 − 4 3 r 3 + 1 = 1 2 r 3 2 − 4 3 r 3 + 1 = 1 2 r 3 2 − 4 3 r 3 + 1 = 0 = 2 4 3 6 4 + 1 4 4 − 8 = 6 3 1 3 − 2 = 3 1 − 3 r 3 = 2 3 4 − 1 3 = 4 3 1 − 2 r 2 = 4 3 1 3 − 3 = 3 2 ( 1 + 1 3 ) Squaring both sides Multiply both sides by 4 Since 3 r 3 − 2 r 1 = 2 3 1
Therefore a + b + c + d + e = 2 + 3 + 1 + 1 + 1 3 = 2 0 .