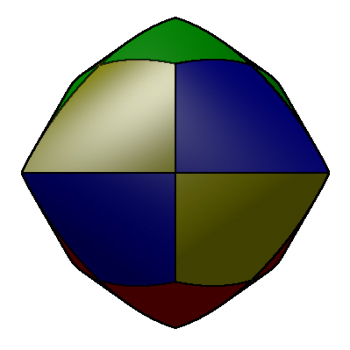
Steinmetz gone wild

Consider the vector field $\vec{F} = (x,y,z)$ . By Ostrogradsky' theorem, $\Phi = \iiint_{W} \vec{\nabla}\cdot\vec{F}\,dV= \iiint_{W} 3\,dV= 3V$ . But we also have $\Phi = \sum_{\text{all sides}} \iint \vec{F}\cdot\vec{n}\,dS = \sum_{\text{all sides}}\iint (x,y,z)\cdot(x,y,0)\,dS = \sum_{\text{all sides}}\iint 1\,dS=A$ . Hence $A=3V$ . So $\boxed{3}$ is the answer.

Note that the answer is independent of the number of cylinders $n \geq 2$ . As long as at least one of the cylinders is distinct, $\frac{A}{V} = 3$ .

Great thanks to prof. Otto Bretscher for the inspiration and a challenging semester of Vector Calculus!

Here is an intuitive, non-rigorous way to solve it: Consider a surface element $dS$ on the boundary of $W$ , which is a surface element on the boundary of one of the intersecting cylinders of radius 1. The pyramid over $dS$ with its apex at the origin will have a volume of $dV = \frac{1}{3} dS$ . Thus $V=\frac{A}{3}$ and $\frac{A}{V}=\boxed{3}$ .

I will provide a rigorous explanation later, unless somebody else beats me to the punch.