Step-Up Rationalization II
(
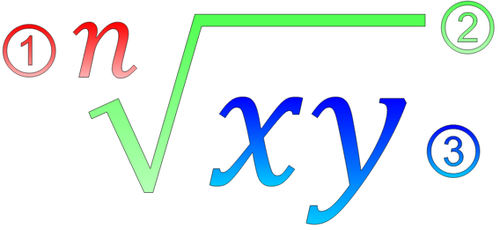5
+
1
)
(
4
5
+
1
)
(
8
5
+
1
)
(
1
6
5
+
1
)
4
Let the above expression be denoted as x , find the value of ( x + 1 ) 4 8 .
Image Credit: Wikimedia nTH root
The answer is 125.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Putting in another way, let
a
=
1
6
5
.
⟹
a
1
6
=
5
Multiplying numerator and denominator by (a-1)
x
=
(
a
8
+
1
)
(
a
4
+
1
)
(
a
2
+
1
)
(
a
+
1
)
(
a
−
1
)
4
(
a
−
1
)
x
=
a
1
6
−
1
4
(
a
−
1
)
=
a
−
1
.
∴
(
x
+
1
)
4
8
=
(
a
−
1
+
1
)
4
8
=
(
1
6
5
)
4
8
=
1
2
5
This is the SAME problem that had appeared some time back.
Actually that was my problem some time ago.
x = ( 5 + 1 ) ( 4 5 + 1 ) ( 8 5 + 1 ) ( 1 6 5 + 1 ) ( 1 6 5 − 1 ) 4 ( 1 6 5 − 1 ) = . . . = 1 6 5 − 1
( x + 1 ) 4 8 = 5 3 = 1 2 5