Step up to the plate
 Find the mass
M
of a metal plate
R
bounded by
y
=
x
,
y
=
x
2
, with density given by
D
(
x
,
y
)
=
1
+
x
y
.
Find the mass
M
of a metal plate
R
bounded by
y
=
x
,
y
=
x
2
, with density given by
D
(
x
,
y
)
=
1
+
x
y
.
The answer is 0.208.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
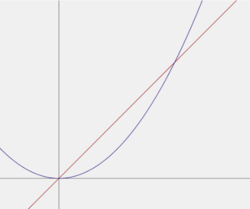
I n t e r s e c t i o n P o i n t s , y = x a n d y = x 2 , ∴ x = x 2 , ⟹ x = 0 , x = 1 . ∴ t h e t w o i n t e r s e c t i o n p o i n t s a r e ( 0 , 0 ) , ( 1 , 1 ) .
d M = ( 1 + x y ) d A = ( 1 + x y ) δ x ∗ δ y . In the vertical strip δ x moves down from y = x , t o y = x 2 , ∴ the strip itself moves from x=0 to x=1...... ⟹ ∫ 0 1 ∫ y = x 2 y = x { 1 + x y } d y d x = 2 5 5 = 0 . 2 0 8 3 3 For dxdy, in the horizontal strip δ y m o v e s f r o m x = y t o x = y . and the strip from 0 to 1, since intersect is at (1,1) . ⟹ ∫ 0 1 ∫ x = y x = y { 1 + x y } d y d x = 2 5 5 = 0 . 2 0 8 3 3
The stuff you can do with random sampling is pretty neato.
Python 2.7:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
|
Also, good to see you're still writing problems!
It is commonly known that the mass of an object is defined as:
Mass = Density ∗ Volume
or in Calculus terms:
M = ∭ Q ρ ( x , y , z ) d V
ρ ( x , y , z ) : density function
d V : differential volume
Q : bounded volume
However, since we are dealing in the 2 dimensional xy plane the equation reduces to:
M = ∬ R ρ ( x , y ) d A = ∫ a b ∫ h 1 ( x ) h 2 ( x ) ρ ( x , y ) d y d x
where the bounds of x,y are are:
a ≤ x ≤ b and h 1 ( x ) ≤ y ≤ h 2 ( x )
The x bounds of this problem can simply be found as the x-coordinates of the intersection between the functions (hence, their equality):
x = x 2 ⇒ x = 0 , 1
The y bounds of the inner integral are represented as a function of x, and as usual, you must always subtract the lower function from the upper one to find the positive area.
And in this case:
x 2 ≤ x { x ∣ 0 ≤ x ≤ 1 }
Given our density function:
ρ ( x , y ) = 1 + x y
Substituting into our earlier double integral equation we get:
∫ 0 1 ∫ x 2 x 1 + x y d y d x
Integrating with respect to y (remember to treat x as a constant) :
⇒ ∫ 0 1 ( y + 2 x y 2 ) ∣ ∣ ∣ ∣ ∣ ∣ x 2 x d x
Substituting in the bounds of the inner integral:
⇒ ∫ 0 1 ( ( x ) + 2 x ( x ) 2 ) − ( ( x 2 ) + 2 x ( x 2 ) 2 ) d x
And after some simplification:
⇒ ∫ 0 1 2 − x 5 + 2 x 3 − x 2 + x d x
Further integrating once more, but this time with respect to x:
⇒ ( 1 2 − x 6 + 8 x 4 − 3 x 3 + 2 x 2 ) ∣ ∣ ∣ ∣ ∣ ∣ 0 1
Substituting the final bounds and approximating:
= 2 1 + 8 1 − 3 1 − 1 2 1 = 2 4 5 ≈ 0 . 2 0 8 3 3 3 3 3 . .
This is one of my few solutions, so please let me know of any improvements I can make =)