Stephen's Birthday
It is Stephen's birthday and he has a circular cake with which he wishes to place candles upon. Like most people he struggles to judge fractions such as thirds so can only split distances in half. For example, he can place 4 candles in a concentric circle (in relation to the cake) by halving and then halving again, and can also place a single candle in the centre if he were 5, as shown below.
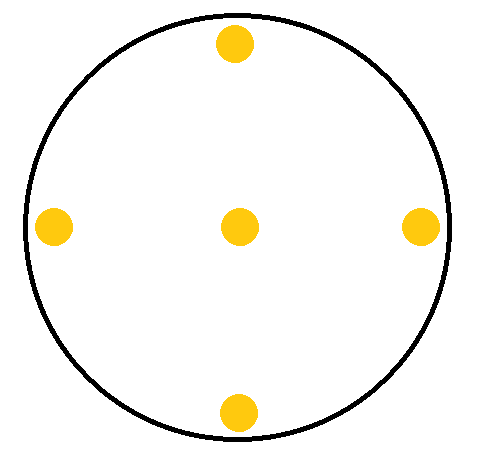
Can Stephen place candles on the cake for all ages between 10 and 100 (by only halving the distances in multiple concentric circles in which every circle has a different number of candles)?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Each concentric circle will have a power of 2 number of candles, and each circle will have a different power of 2 number in it. This turns the problem into which integers can be expressed as the sum of different powers of 2, to which the answer is Yes as all numbers can be written in binary.