Stick the circle mechanics
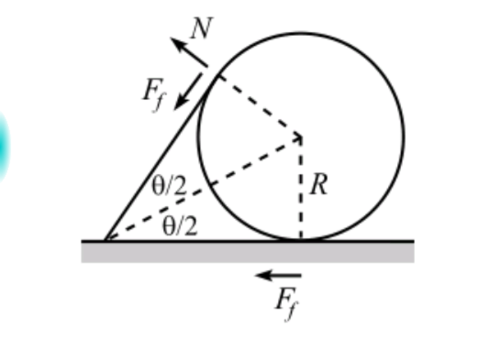
a stick of mass density 'Q' per unit length rests on a circle of radius 'R' . the stick makes an angle
with the horizontal and is tangent to the circle at its upper end . Friction exists at all points of contact and assume that it it is large enough to keep the system at rest . Find frictional force between ground and circle.
- radius is 2 m and
- take g's value as 10 .......... 9.8 will not give correct answer
-
is 60 degrees
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Considering first the forces on the circle, taking moment about the centre O tells us that the frictional forces at the two points of contact are the same. Resolving forces horizontally gives F + F cos 6 0 ∘ = R 2 cos 3 0 ∘ and hence R 2 = F 3 .
Now considering forces on the rod, taking moments about X tells us that R 2 × L = W 1 × 2 1 L cos 6 0 ∘ and hence R 2 = 4 1 W 1 , and hence F = 4 3 W 1 , where L = 2 3 is the length of the rod, and W 1 = Q L g is the weight of the rod. Thus F = 2 1 Q g = 5 Q .
Interestingly, resolving forces on the rod horizontally tells us that F 3 = F as well.