Stop and Think!
If the above quadratic equation has distinct real roots in for real numbers and with non-zero , then what can you say about the sign of and ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
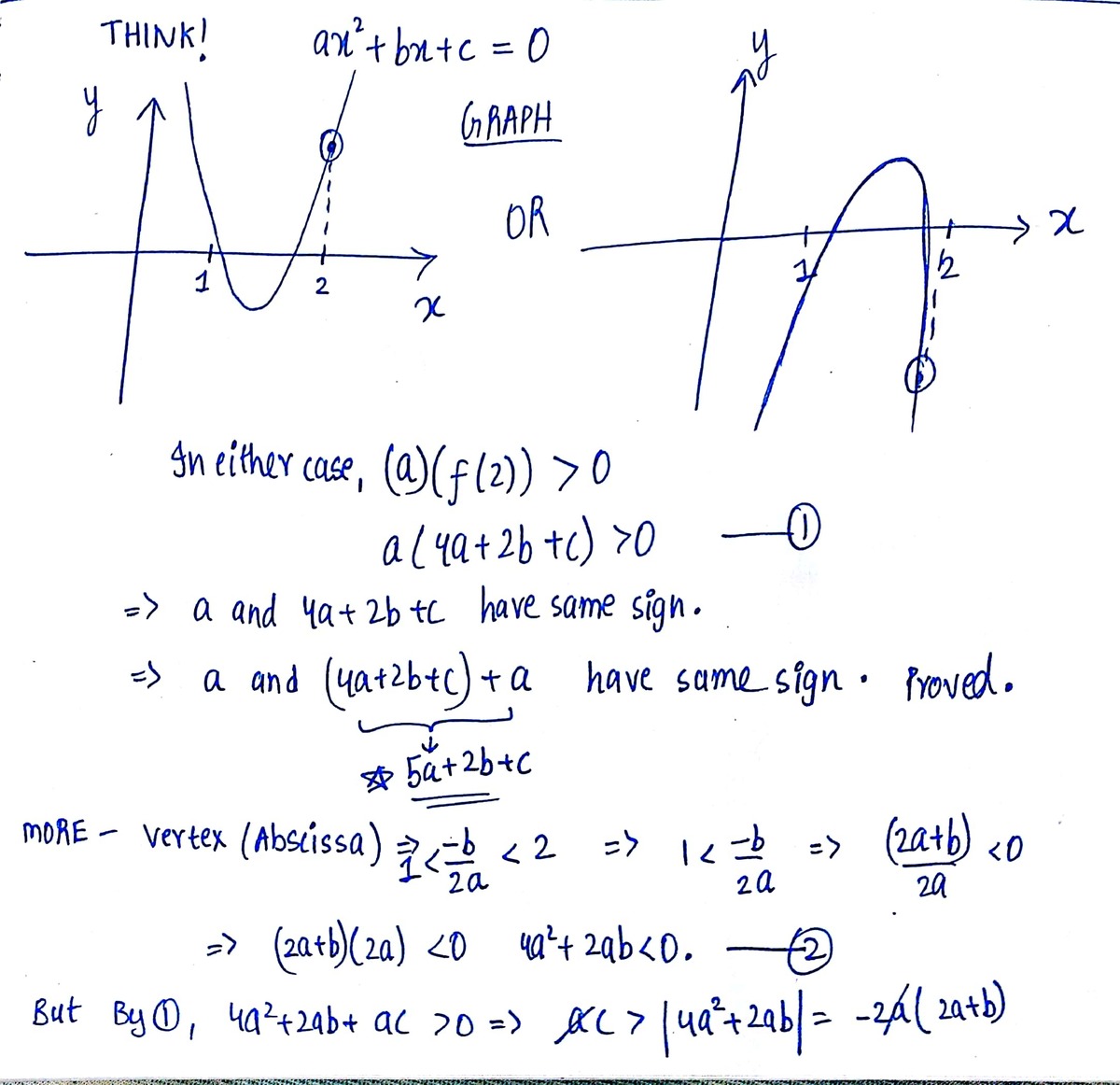

Say α , β are the roots of the given equation. Now considering, 5 a + 2 b + c . Since a = 0 , therefore, it is legitimate to divide this expression by a . Dividing 5 a + 2 b + c by a yields 5 − 2 ( − a b ) + a c . Since a − b = α + β and a c = α ⋅ β , therefore we have 5 − 2 ( α + β ) + α ⋅ β . After some simple manipulations, 5 − 2 ( α + β ) + α ⋅ β can be written as ( α − 2 ) ( β − 2 ) + 1 . Since α , β ϵ ( 1 , 2 ) , therefore, ( α − 2 ) ( β − 2 ) > 0 . Consequently, ( α − 2 ) ( β − 2 ) + 1 > 1 . So, a 5 a + 2 b + c > 1 . Clearly, this is possible only when 5 a + 2 b + c and a have the same sign.